Games101-现代计算机图形学入门-Transformation
Transformation
Linear Algebra
- 点乘(投影,判断两个向量方向相同、距离远近)
- 叉乘 (判断点p是否在三角形▲ABC内,AB、BC、CA分别和AP、BP、CP叉乘,都在同一边则在三角形内)
Modeling
- translation
- rotation
- scale
- 仿射变换 = 线性变化 + 平移(先做线性变化再做平移)
二维变换

对二维矩阵加一维以便计算平移,是0则表示向量,是1则表示点,(1,0,1)和(2,0,2)是同一个点
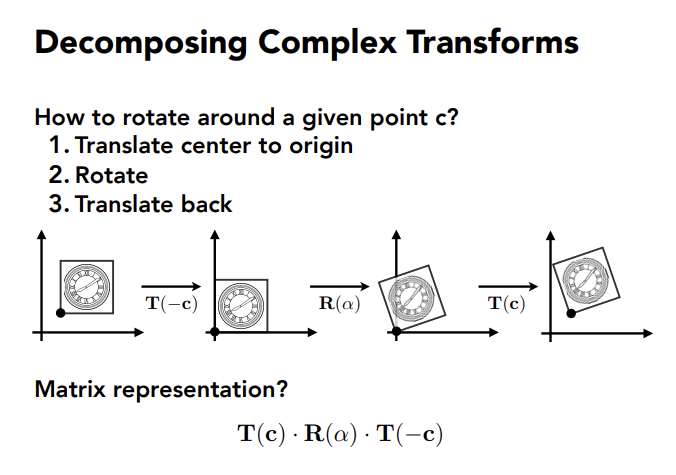
平移后旋转 != 旋转后平移 即 矩阵不满足交换律
多个变换可合并成一个矩阵,一个矩阵也可以拆成多个变换
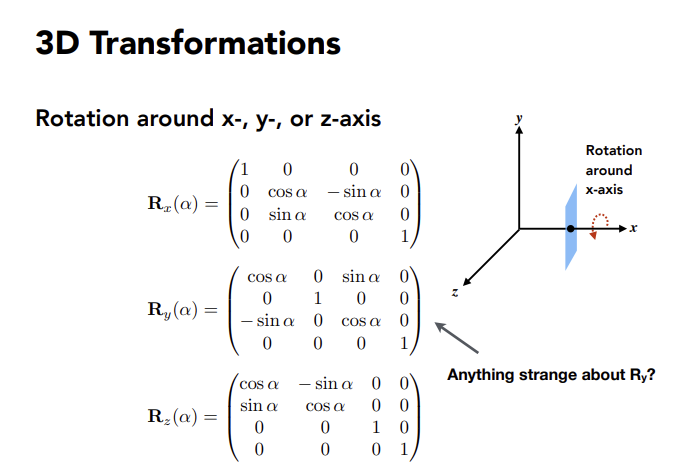
三维变换
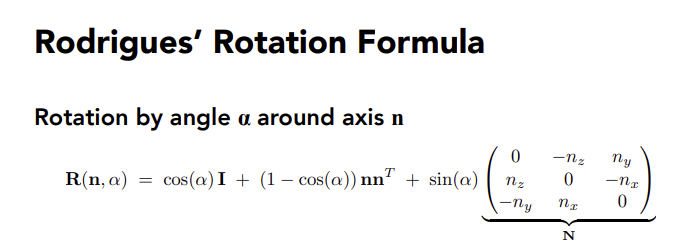
Viewing
视图变换 view transformation
相机通过3个值确定
- 向上的方向
- 坐标
- 看向的位置
相机和场景一起移动,直到相机在一个特定的位置(通常为原点,Y为竖直方向,相机看向-Z)
此操作中的旋转从随即方向到坐标轴方向的转换矩阵A比较难求,但从坐标轴到某随即方向的矩阵B好求,这个矩阵是正交矩阵且是A的逆矩阵,则A为B的转置
投影变换 projection transformation
正交投影 Orthographic projection
- 平移
- 缩放到cube[-1,1]上
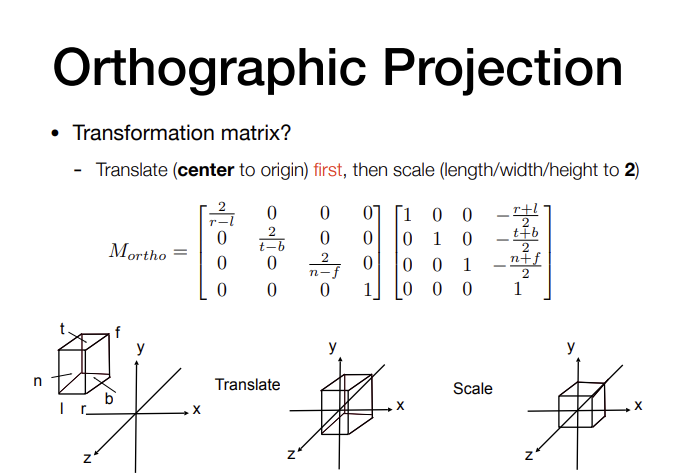
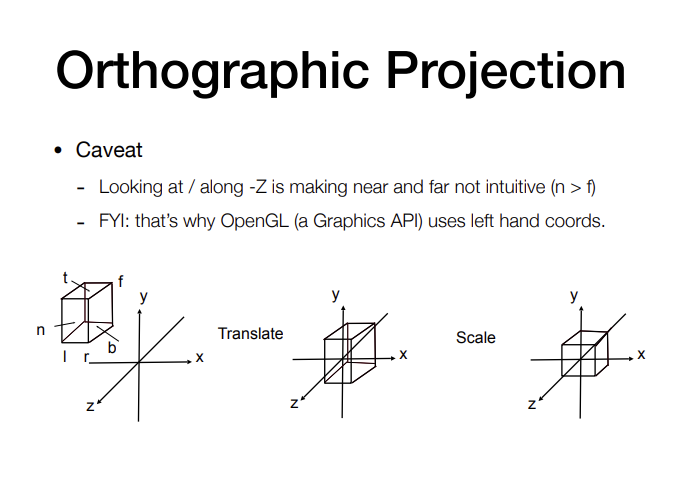
透视投影 Perspective projection
满足进大远小,先做透视变换,再做正交变换
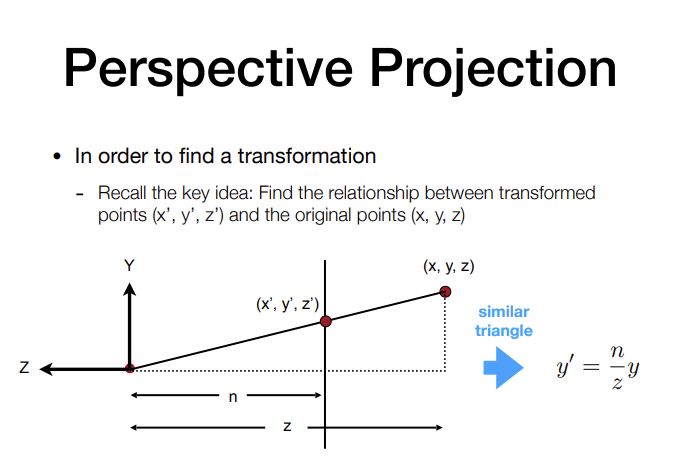
x,y的变换通过相似三角形可以得出
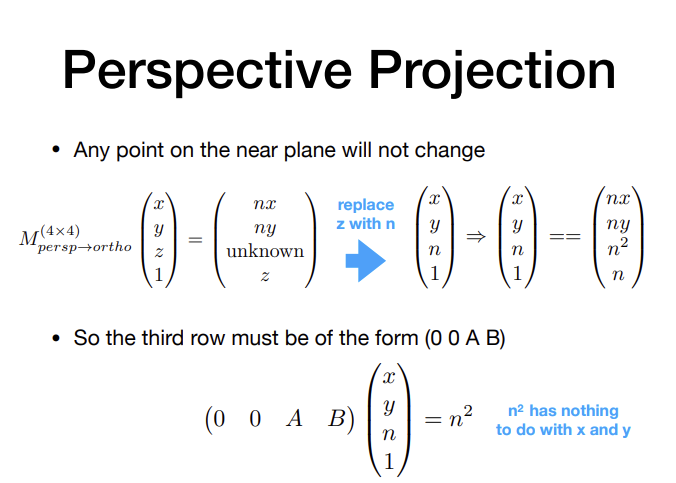
对于近平面n和远平面f,Z轴是不变的。但是在中间的点Z是变化的,因此对于Z的变换先假设未知,然后通过n,f的特例解方程
 |
 |
|---|---|
 |
 |
 |
 |



