ADB-数据库基本概念
数据库基本术语概念
超码
在关系中能唯一标识一个元组的属性集称为关系模式的超码
因为通过id可以找到唯一一个学生,所以{id}是一个超码,同理{id,student_number}、{id,student_number,name}、{id,student_number,name,sex}、{student_number}、{student_number,name}、{student_number,name,sex}也是超码.
候选码
- 不含多余属性的超码
- 包含在候选码中的属性称为主属性(Primary Attribute)
- 不包含在任何一个候选码中的属性称为非主属性(Nonprime Attribute)
在上例中,只有{id}或者{student_number}是候选码。如果sex和name可以唯一标识一个学生,则{name,sex}也为候选码,但是,sex和name并不能唯一标识一个学生,这与现实生活是违反的,因为现实有同名同姓的人,则{name,sex}不能作为候选码。
主码
用户选作元组标识的一个候选码称为主码,其余的候选码称为替换码 (Alternate Key)
关系模式的形式化定义
R(U,D,dom,F)
R为关系模式名,U是一个属性集,D是U中属性的值所来自的域, Dom是属性向域的映射集合,F是属性间的依赖关
例如:
Student关系模式的定义 Student(U,D,dom,F)
U={sno,name,age}
D={CHAR,INT}
Dom={dom(sno)=dom(name)=CHAR,dom(age)=INT}
F={sno→name, sno→age}
函数依赖 FD
若在一张表中,在属性(或属性组)X的值确定的情况下,必定能确定属性Y的值,那么就可以说Y函数依赖于X,写作 X → Y
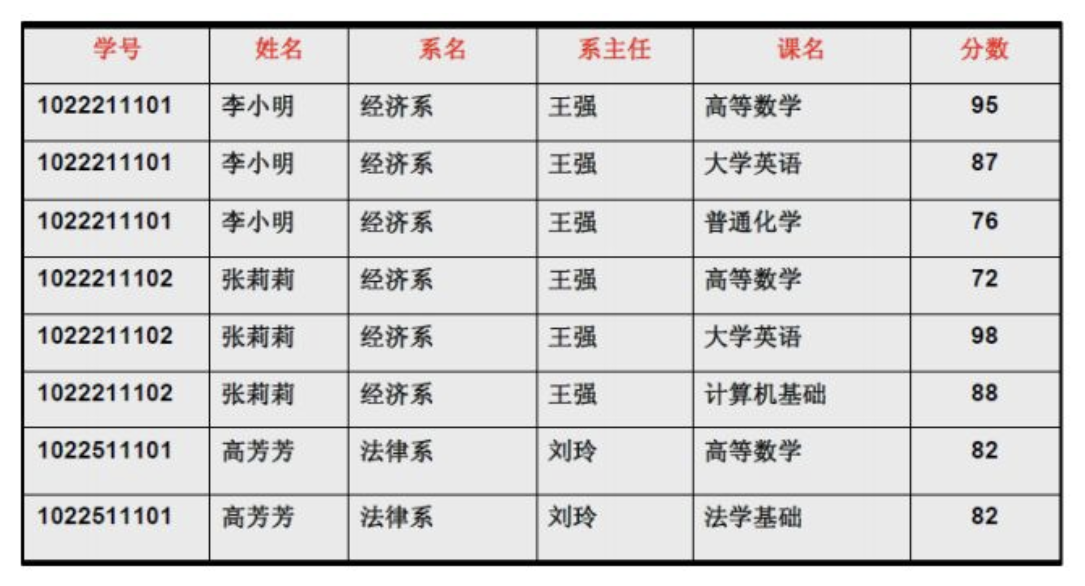
上图中
- 系名 → 系主任
- 学号 → 系主任
- (学号,课名) → 分数
完全函数依赖
在一张表中,若 X → Y,且对于 X 的任何一个真子集(假如属性组 X 包含超过一个属性的话),X ‘ → Y 不成立,那么我们称 Y 对于 X 完全函数依赖
上图中
- 学号 F→ 姓名
- (学号,课名) F→ 分数 (注:因为同一个的学号对应的分数不确定,同一个课名对应的分数也不确定,必须要这两个才能确定分数)
部分函数依赖
假如 Y 函数依赖于 X,但同时 Y 并不完全函数依赖于 X,那么我们就称 Y 部分函数依赖于 X
上图中
- (学号,课名) P→ 姓名 (学号可以确定姓名,课名不能确定姓名)
传递函数依赖
假如 Z 函数依赖于 Y,且 Y 函数依赖于 X ,则 Z 传递函数依赖于 X
ArmStrong公理
自反律(Reflexity):若B ⊆ A,则A→B成立
增广律(Augmentation):若A→B,则AC→BC(AC 表示A∪C)
传递律(Transitivity):若A→B, B→C,则A→C
自含律(Self_Determination): A→A
分解律(Decomposition):若A→BC,则A→B,且 A→C
合并律(Union):若A→B, A→C,则A→BC
复合律(Composition):若A→B, C→D,则AC→BD
闭包
设F是属性集U上的一个FD集,X是U的子集,则称所有用Armstrong推理规则推出的函数依赖 X→A中所有A的集合,称为属性集X关于F的闭包 ,记做X+
例如:
F={A→B, B→C, B→D, A→D }
A+=ABCD
B+=BCD
C+=C
D+=D
最小函数依赖集
给定一个函数依赖集S,若能找到一个远小于S的等价函数依赖集T,则DBMS只要实现T就可实现S中的所有函数依赖
- F的每个FD的右边只有一个属性
- F不可约:F中的每个X→Y,F-{X→Y}与F不等价
- F的每个FD的左部不可约:删除左边的任何一个属性都会 使F转变为一个不等价于原来的F的集合
例如:
R(A,B,C,D),F={A→BC, B→C, A→B, AB→C, AC→D}
将右边写出单属性并去除重复FD(分解律)
F={A→B, A→C, B→C, A→B, AB→C, AC→D}
F={A→B, A→C, B→C, AB→C, AC→D}
消去左部冗余属性
A→C, AC→D可推出A→AC, A→D,因此可去除AC→D中的C
A→C,可推出AB→BC可得AB→C ,所以AB →C中的B是冗余属性
F={A→B, A→C, B→C, A→C, A→D}
={A→B, A→C, B→C, A→D}
消去冗余函数依赖
A→C冗余,因为可由A→B, B→C推出
F={A→B, B→C, A→D}
关系代数

SELECT S1#, S2#
FROM (Select S# AS S1#,city From S) S1, (Select S# AS S2#,city From S) S2
WHERE S1.city = S2.city AND S1.S1# < S2.S2#
选择(selection)运算:σ
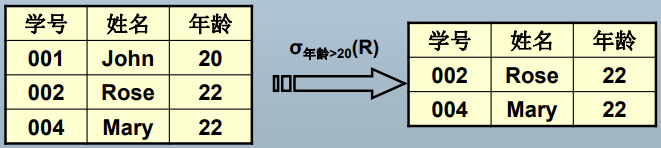
投影(projection)运算:π
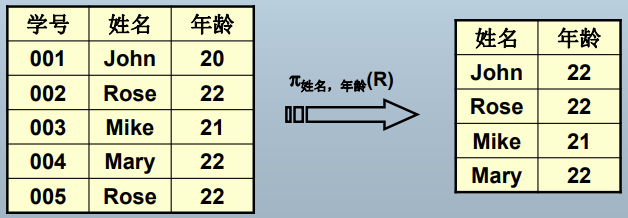
连接(join)运算:⋈
自然连接
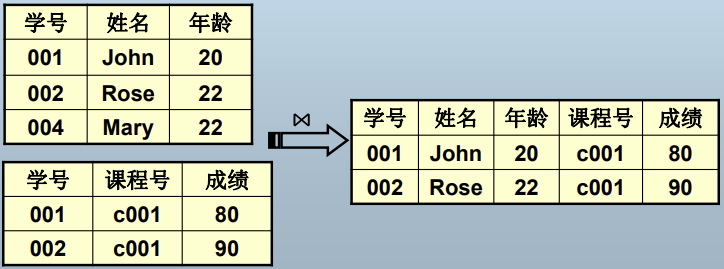
θ链接
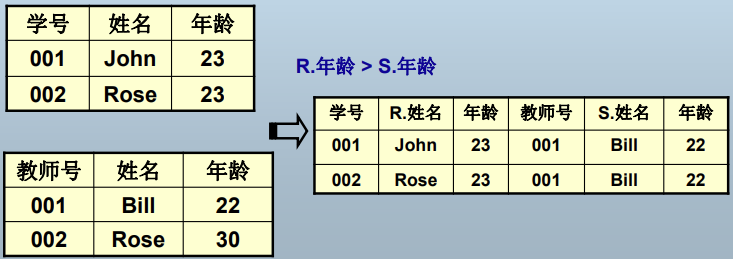
等值连接
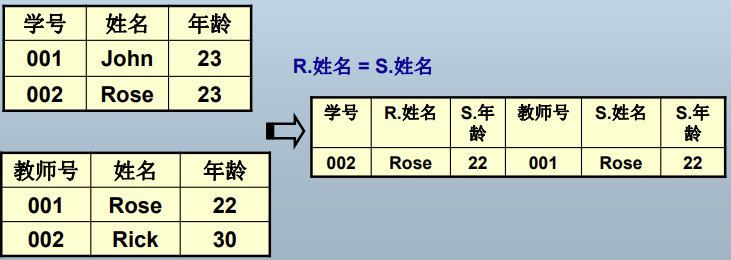
重命名:ρx(E)
x是E结果的新名字




