ADB-三大范式以及BCNF
数据库三大范式以及BCNF
第一范式 1NF
每个属性不可再分
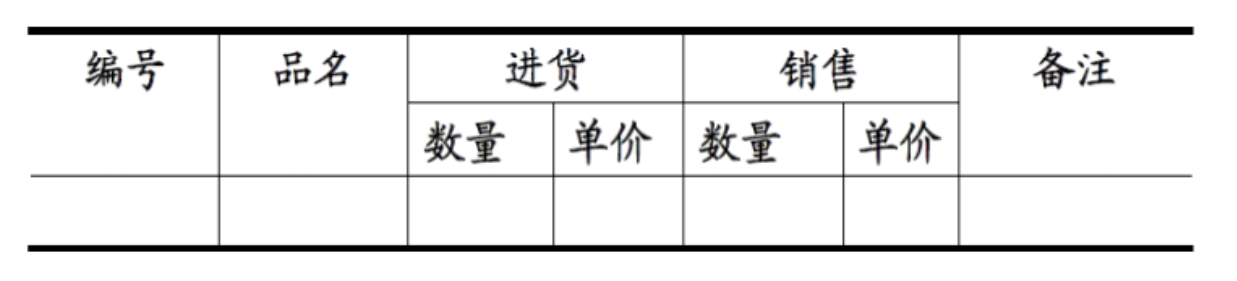
上图不满足1NF
可以将其拆开
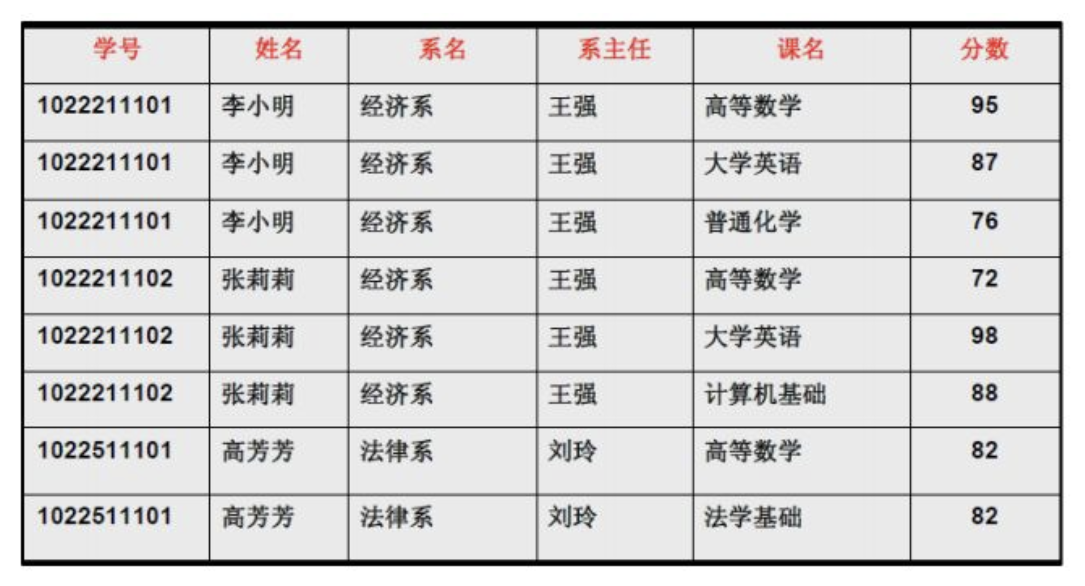
但是数据冗余过大,且有添加系的信息必须要有学生,删除学生主任也跟着删除等问题
第二范式 2NF
看数据表中是否存在非主属性对于码的部分函数依赖
- 找出数据表中所有的码
- 根据第一步所得到的码,找出所有的主属性
- 数据表中,除去所有的主属性,剩下的就都是非主属性了
- 查看是否存在非主属性对码的部分函数依赖
第一步:找到码(学号,课名)
第二步:主属性 学号 和 课名
第三步:非主属性 姓名、系名、系主任、分数
第四步:
对于(学号,课名) → 姓名,有 学号 → 姓名,存在非主属性 姓名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系名,有 学号 → 系名,存在非主属性 系名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系主任,有 学号 → 系主任,存在非主属性 对码(学号,课名)的部分函数依赖。
为了满足2NF,可以进行模式分解拆分成两个表
选课(学号,课名,分数)
学生(学号,姓名,系名,系主任)
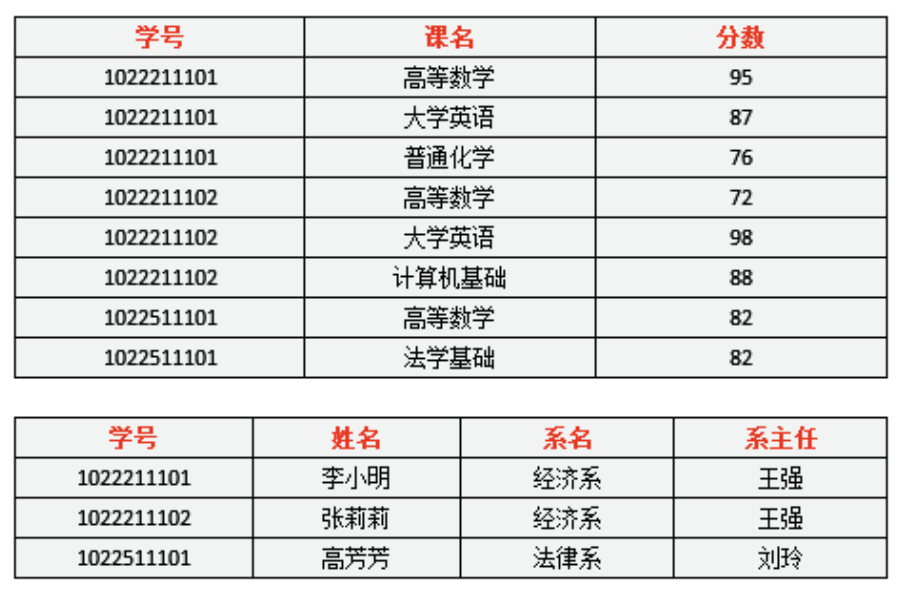
但如果删除某个系所有学生记录,则该系丢失
插入一个无学生的新系,无法操作
第三范式 3NF
当且仅当R属于2NF,且R的每一个非主属性都不传递依赖于主码时,R∈3NF
对于选课表,主码为(学号,课名),主属性为学号和课名,非主属性只有一个,为分数,不可能存在传递函数依赖,所以选课表的设计,符合3NF的要求。
对于学生表,主码为学号,主属性为学号,非主属性为姓名、系名和系主任。因为 学号 → 系名,同时 系名 → 系主任,所以存在非主属性系主任对于码学号的传递函数依赖,所以学生表的设计,不符合3NF的要求
为了让数据表设计达到3NF,我们必须进一步进行模式分解为以下形式:
选课(学号,课名,分数)
学生(学号,姓名,系名)
系(系名,系主任)
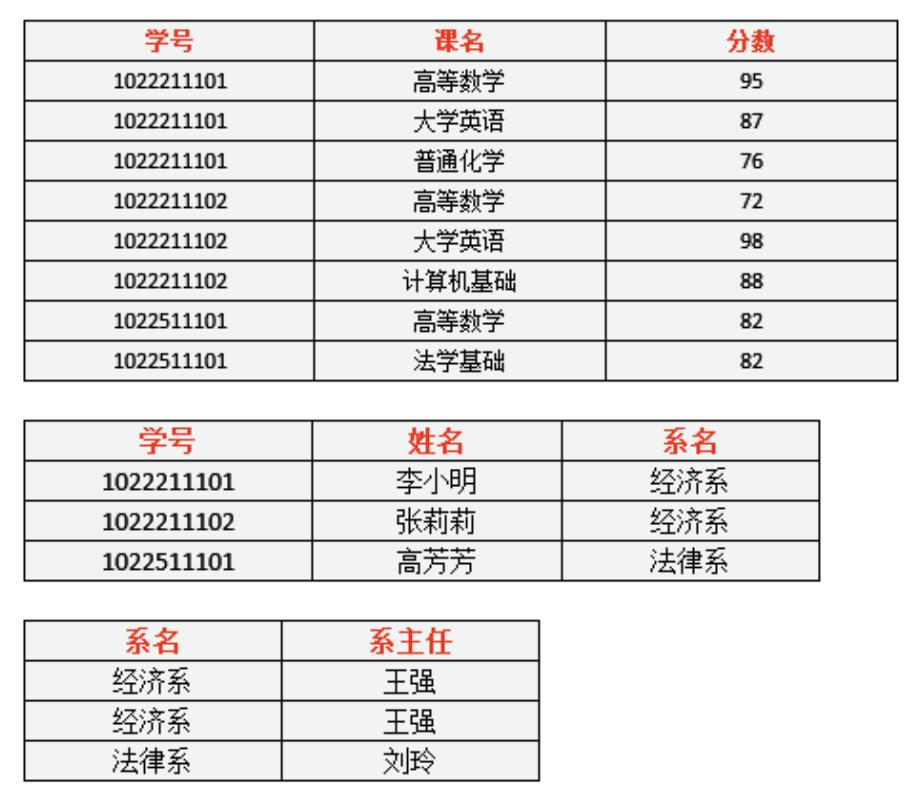
1NF,2NF的问题基本解决,3NF符合数据库设计要求
BCNF
消除主属性对于码的部分与传递函数依赖
若:
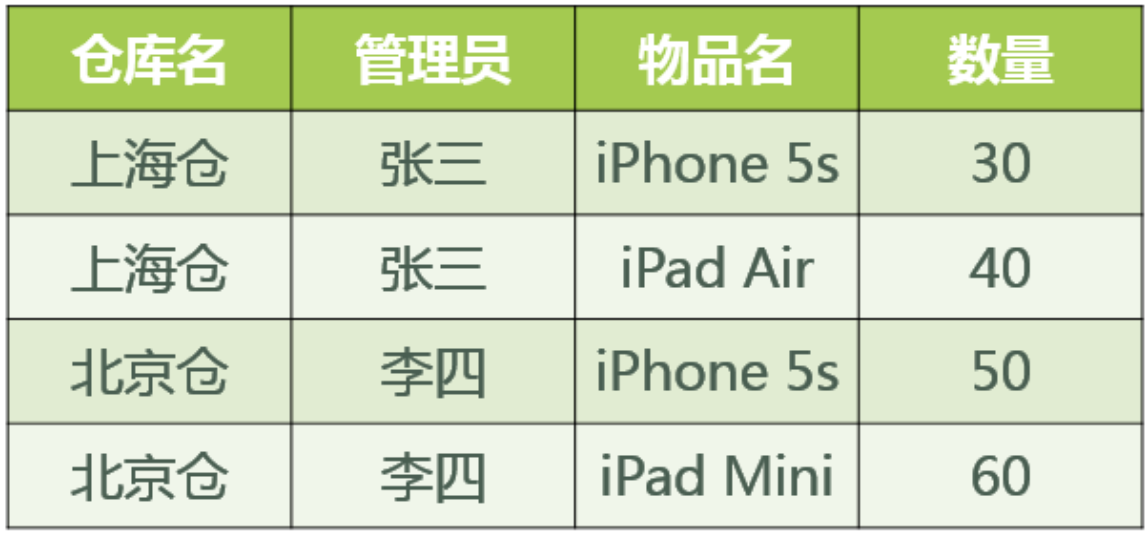
- 某公司有若干个仓库;
- 每个仓库只能有一名管理员,一名管理员只能在一个仓库中工作;
- 一个仓库中可以存放多种物品,一种物品也可以存放在不同的仓库中。每种物品在每个仓库中都有对应的数量。
已知函数依赖集:
仓库名 → 管理员,管理员 → 仓库名,(仓库名,物品名)→ 数量
码:(管理员,物品名),(仓库名,物品名)
主属性:仓库名、管理员、物品名
非主属性:数量
∵ 不存在非主属性对码的部分函数依赖和传递函数依赖。
∴ 此关系模式属于3NF。
- 先新增加一个仓库,但尚未存放任何物品,是否可以为该仓库指派管理员?——不可以,因为物品名也是主属性,根据实体完整性的要求,主属性不能为空。
- 某仓库被清空后,需要删除所有与这个仓库相关的物品存放记录,会带来什么问题?——仓库本身与管理员的信息也被随之删除了。
- 如果某仓库更换了管理员,会带来什么问题?——这个仓库有几条物品存放记录,就要修改多少次管理员信息。
造成此问题的原因:存在着主属性对于码的部分函数依赖与传递函数依赖。(在此例中就是存在主属性【仓库名】对于码【(管理员,物品名)】的部分函数依赖。
解决办法就是要在 3NF 的基础上消除主属性对于码的部分与传递函数依赖。
应分解成
仓库(仓库名,管理员)
库存(仓库名,物品名,数量)
模式分解
无损连接且保持函数依赖地分解到3NF
算法1:保持函数依赖地分解到3NF
- 求出R<U,F>的最小函数依赖集(仍记为F)
- 把所有不在F中出现的属性组成一个关系模式R’, 并在U中去掉这些属性(剩余属性仍记为U)
- 若F中存在X→A,且XA=U, 则输出R(U)和R’,算法结束,否则
- 对F按相同的左部分组,将所有X →A1, X →A2,…, X→Ak形式的FD分为一组,并将每组涉及的所有属性作为一个关系模式输出。若某个关系模式Ri的属性集是另一个关系模式的属性集的子集,则在结果中去掉Ri。设最后得到关系模式R1,R2,…,Rk,则p={R1,R2,…,Rk,R’}一个保持函数依赖的分解,并且满足3NF
R(S#,SN,P,C,S,Z)
F={S#→SN,S#→P,S#→C,S#→S,S#→Z,{P,C,S}→Z,Z→P,Z→C}
- 求出最小FD集:F={S#→SN,S#→P,S#→C,S#→S,{P,C,S}→Z,Z→P,Z→C} // S# →Z冗余
- q={R1(S#,SN,P,C,S),R2(P,C,S,Z),R3(Z,P,C)}
- R3是R2的子集,所以去掉R3 q={R1(S#,SN,P,C,S),R2(P,C,S,Z)}
- R的主码为S#,于是 p=q ∪ {R(X)}={R1(S#,SN,P,C,S),R2(P,C,S,Z),R(S#)}
- 因为{S#}是R1的子集,所以从p中去掉R(S#)
- p={R1(S#,SN,P,C,S),R2(P,C,S,Z)}即最终结果
无损连接分解到BCNF
输入:R
输出:p={R};
检查p中各关系模式是否都属于BCNF,若是,则算法终止
设p中S(U
s)非BCNF关系模式,则必存在X→A,其中 X不是S的超码① 将S分解为S1(XA)和S2(U
s-A),此分解是无损连接的 //({XA}∩{Us-A}=X)→(A={XA}-{Us-A})② p={p-S} ∪ {S1, S2};//用S1和S2替换p中的S
③ 转到第2步;
由于U的属性有限,因此有限次循环后算法终止
例如:
R(S#,C#,G,TN,D), F=




