Materials and Appearances

Materials=BRDF

Diffuse/Lambertian Material 漫反射材质

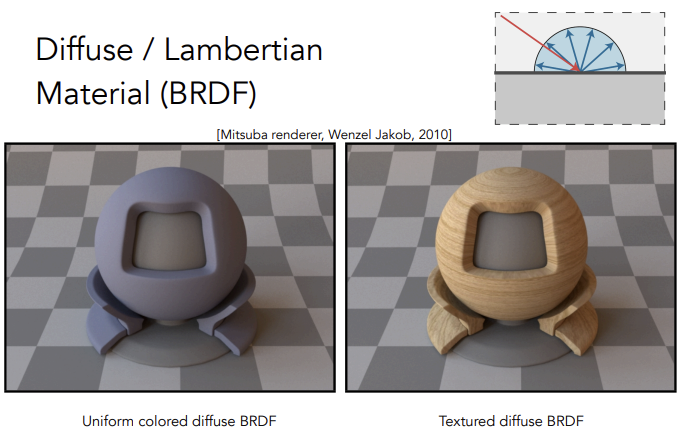
在Blinn-Phong模型中，讨论漫反射系数的时候，我们只是经验性的引入 $I/r^2$ 来表示到达着色点的能量，但这并不准确

根据渲染方程可推出

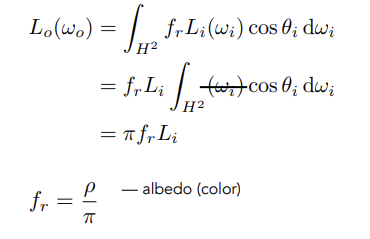
Ideal reflective/refractive material 理想反射/折射材质

光线到达材质表面被吸收一部分，同时发生镜面反射和镜面折射

Perfect Specular Reflection 镜面反射

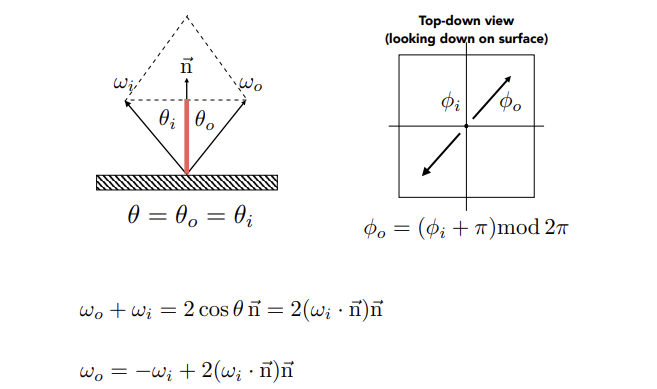
公式分为两部分，左图（正视图）观察入射角和出射角，右图（俯视图）观察方位角

Glossy material 光滑金属

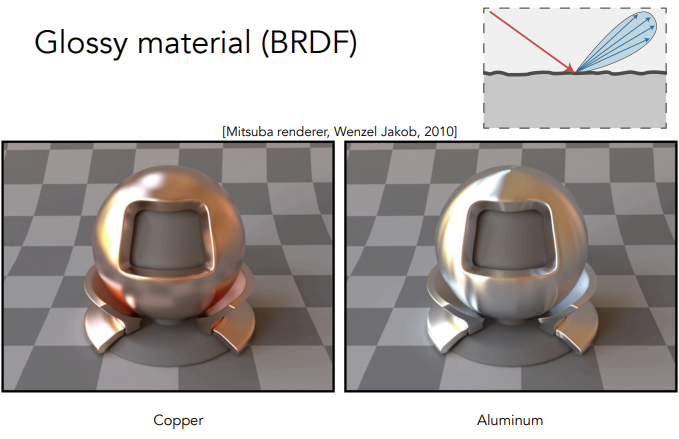
Specular Refraction 镜面折射

Snell‘s Law

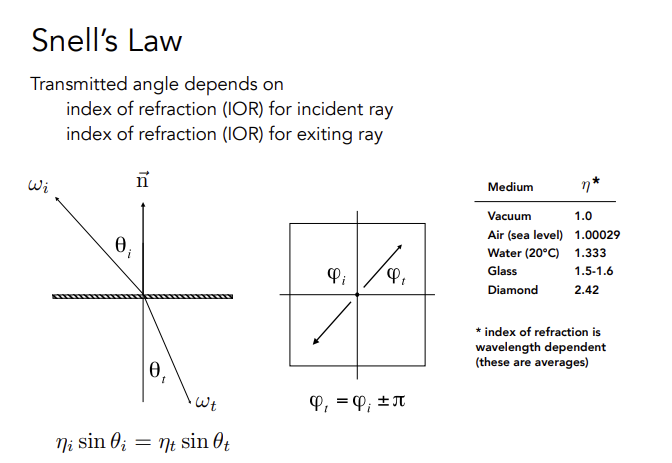
入射材质折射率 × 入射角正弦 = 出射材质折射率 × 折射角正弦

进一步推导

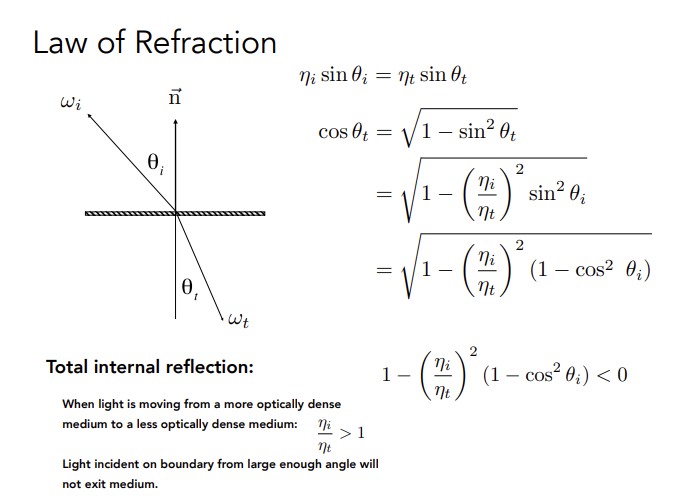
若入射材质折射率 > 出射材质折射率，就会发生全反射

Snell’s Window/Circle

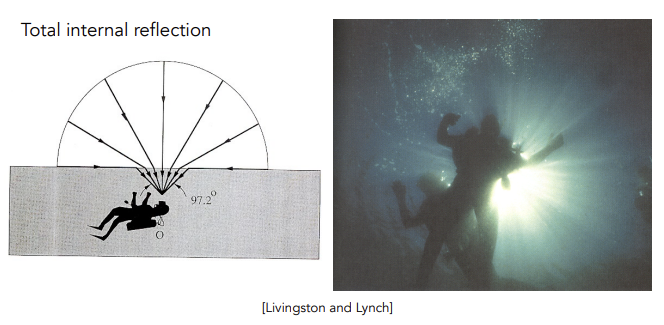
水中只能有锥形视野

双向散射分布函数（BSDF）

描述反射的分布函数被称为双向反射分布函数（BRDF），那么描述折射也需要一种分布函数

这种分布函数被称为双向折射(透射)分布函数（BTDF）

BRDF和BTDF统称为双向散射分布函数（BSDF）

Fresnel Term 菲涅尔项

我们很容易发现，当我们用几乎垂直的视角看下去，基本看不到什么反射，而当我们的视角几乎水平时，反射结果特别明显

这是因为光线以不同角度入射会有不同的反射率，也就是所谓的菲涅尔效应

例如：正对着窗子看能看清窗外景色，侧着看窗外看到大多室内的反射站在湖边，透过近处的湖水能看见水底的情况，而望向远处只能看到群山的倒影

折射率为1.5的绝缘体	导体

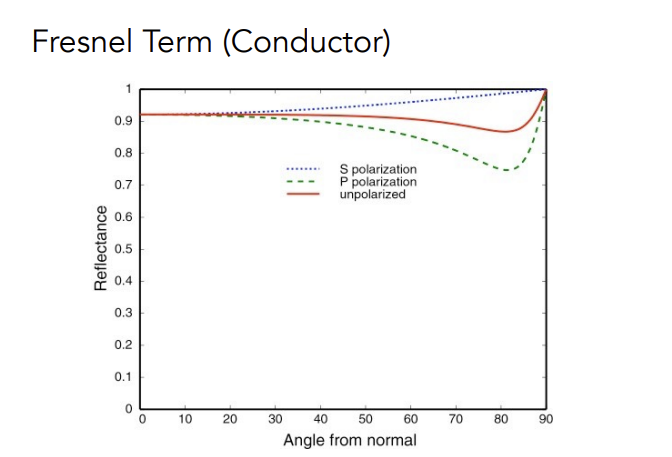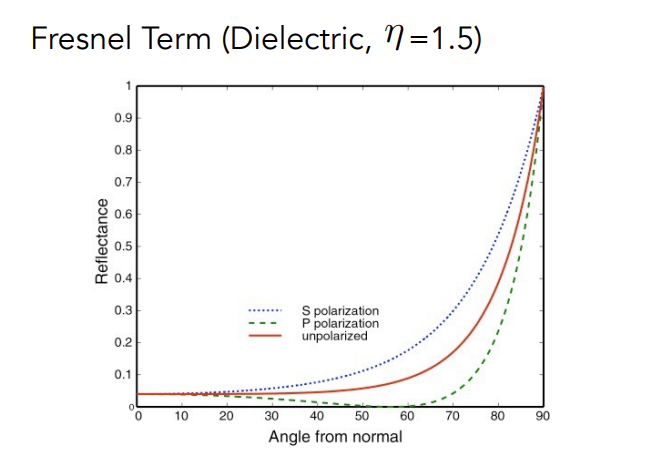
图中另外两条虚线表示光的极化性质，即光只沿一个方向振动情况下的菲涅尔项，现在的渲染器很少考虑这种情况

由图对应到现实一目了然，生活中各种金属的反射率一直都很高，所以我们习惯用镀银的玻璃作为镜子而不是用玻璃

为了计算菲涅尔项，有非常复杂的公式，通过极化的菲涅尔数据做平均得到结果

但我们也有简单的近似（施利克近似 Schlick’s approximation），如图

这种近似方法认为菲涅尔曲线就是一条从 0°入射角菲涅尔项到90°入射角的单调增函数，90°时R0=1

Microfacet Material 微表面模型

大陆崎岖不平，但在远处看像是镜面反射

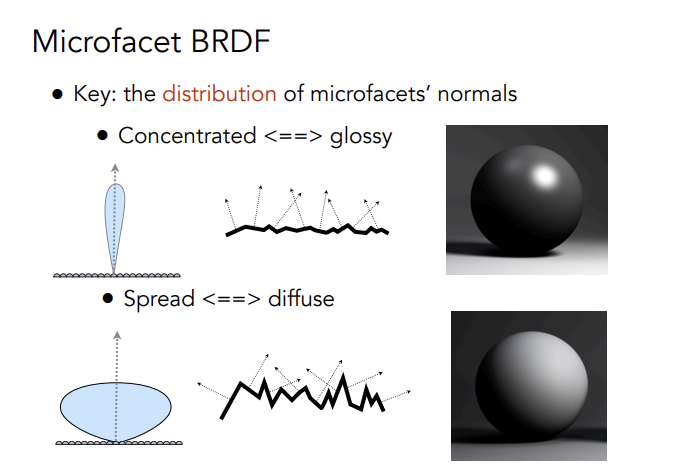
研究发现分布来描述物体粗糙程度

镜面反射法线方向集中，漫反射表面法线分散

由此得出微表面下更精确的BRDF方程

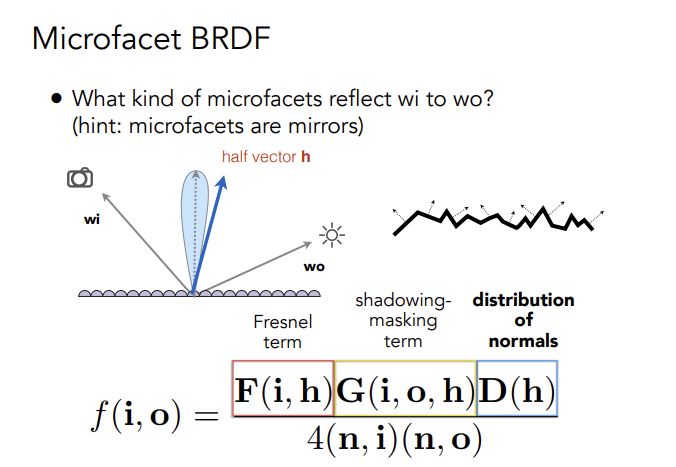
F为菲涅尔项，D为发现分布，G为几何项（在微表面上存在崎岖不平的地方相互遮挡，G起到修正作用）

微表面模型可以得到非常真实的渲染结果，因为他本身就是基于物理的渲染（PBR/PBS）

Isotropic/Anisotropic Materials 各向同性/各向异性材质

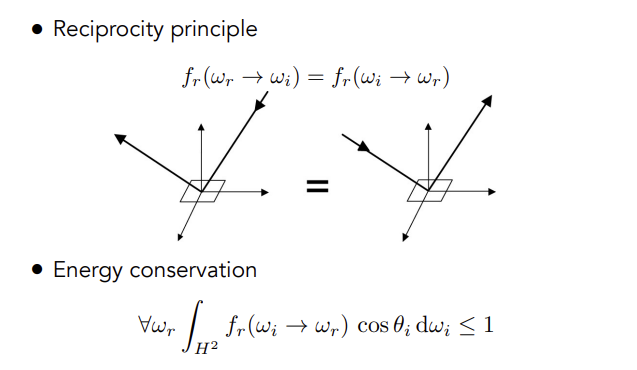
BRDF性质总结

非负/线性（可拆开相加）	可逆/能量守恒

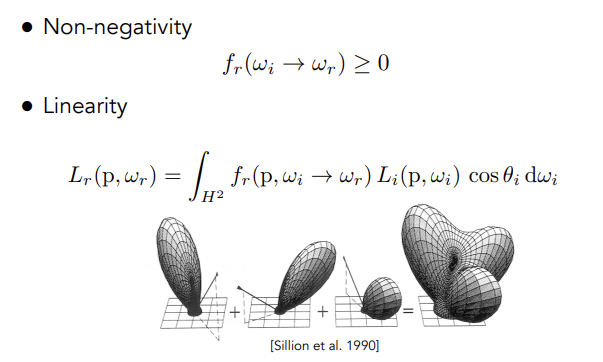BRDF的测量

给定一个着色点，通过改变入射和出射的角度（改变光源与相机位置）进行测量

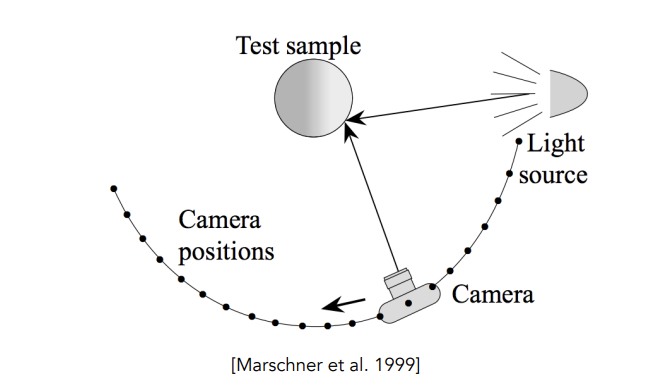
foreach outgoing direction wo
	move light to illuminate surface with a thin beam from wo
	for each incoming direction wi
		move sensor to be at direction wi from surface
		measure incident radiance

为了提高效率，我们可以尽量让材质呈各向同性就像之前说的，这不仅可以让BRDF从四维降至三维，