Games101-现代计算机图形学入门-Animation
Animation
Physical Simulation
Mass Spring System
质点弹簧系统
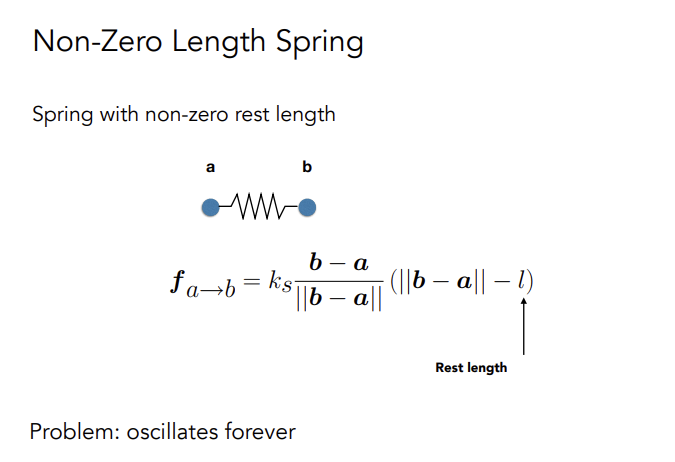
理想弹簧没有初始长度,现实中非零长弹簧
 |
 |
|---|
$(b-a)/||b-a||$为归一化力的方向,但是没有考虑能量损失,弹簧会一直运动
如果简单引入摩擦力,所有运动都会停止,而我们只想停止a和b的相对运动

红框内表示a和b的相对速度在二者连线方向上的投影
应用上述两个质点的相互作用到弹簧系统
 |
 |
 |
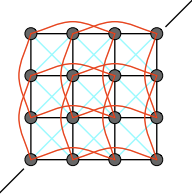 |
|---|
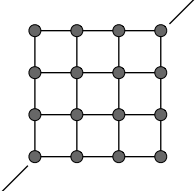
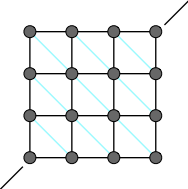
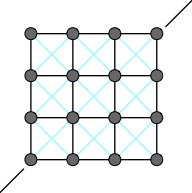
图1,2无法体现抵抗折叠的力(对纸折叠松开后纸会部分恢复),无法体现抵抗拉伸的力(拉一个毛巾松开后毛巾会恢复)
图3改善抗拉伸,图4完善
Finite Element Method(FEM):考虑质点之间的力作用,模拟更加真实但复杂
Particle System
粒子系统广泛用于图形与游戏行业
每个粒子的行为都会被一组人为设置的力所定义,粒子之间常见的作用力举例:重力,电磁力,摩擦力,空气阻力,粘滞力,碰撞等
一般粒子生成步骤如下:
- 生成粒子
- 计算每个粒子的力
- 更新每个粒子的位置和速度
- 将死亡的粒子移除
- 渲染到屏幕
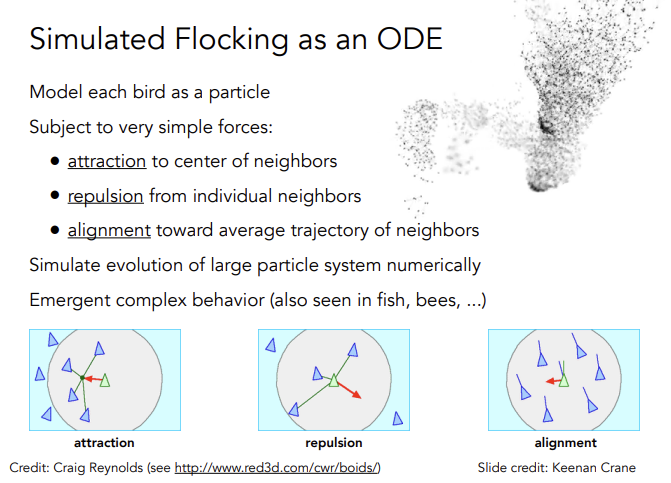
- 鸟会试图融入周边的鸟群
- 鸟之间不会太近
- 都朝一个方向
Single particle simulation
首先假定一个速度场
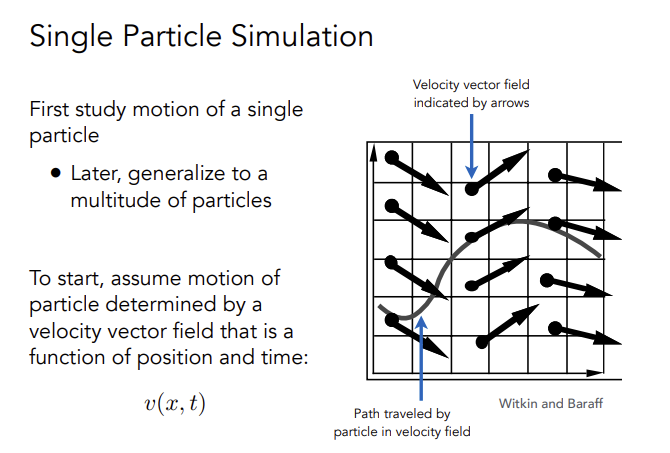
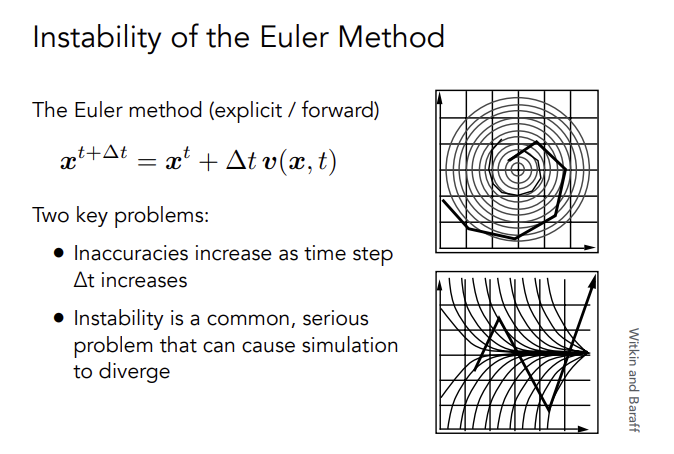
Euler‘s Method
对时间离散化,用前一帧计算结果更新当前帧位置信息
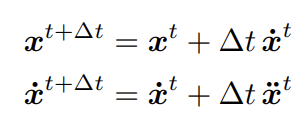
会有误差,且稳定性差
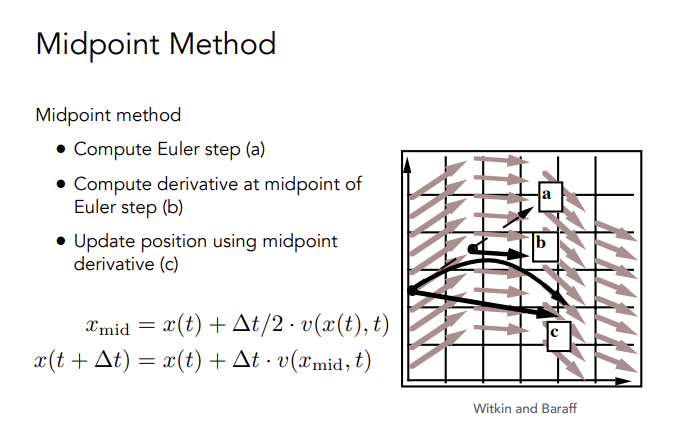
Midpoint Method
做两次欧拉方法,第一次获得中点位置,取中点位置的速度再算一遍欧拉方法
 |
 |
|---|
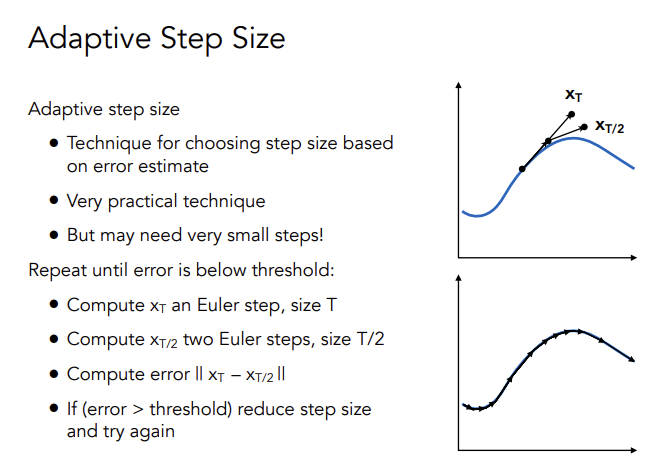
Adaptive Step Size
也是做两次欧拉方法,第一次用Δt算,第二次用Δt/2算,检测两次结果,偏差较大则步长减半重新计算
Implicit Euler Method
后向欧拉方法,用未来的数据计算

Runge-Kutta Family

稳定性:假设步长为h,之前的欧拉方法,截断误差$O(h^2)$,总体误差$O(h)$,而RK4方法可以达到4阶误差
Position-Based/Verlet Integration
如位置调整法,韦尔莱积分等,这些方法通过调整粒子的位置使其满足一些特定性质,虽然不太物理(不满足能量守恒)也不太稳定,但实现起来比较简单,计算也比较快

Rigid body simulation
刚体不发生形变,内部粒子运动方式相同
更多考虑角度,角速度,角加速度等

Fluid simulation
流体模拟认为流体粒子不可压缩,且密度处处相等(变化前后密度也保持不变),那么任何时刻,任意位置的流体粒子发生运动都会导致其周围粒子的密度发生变化(马尔科夫链),而要使运动前后密度不变, 就需要通过改变流体粒子位置来修正
这个修正过程,就是流体模拟的过程
修正方法用到了深度学习的梯度下降法

Material Point Method(MPM)
Lagrangian(质点法):逐个进行单粒子模拟
Eulerian(网格法):将空间定义为多个网格单元,通过观察网格决定如何模拟
将二者结合,认为粒子具有一些属性,存储在粒子上,然后用网格法模拟,最后将每个时刻网格信息写回粒子上
Kinematics
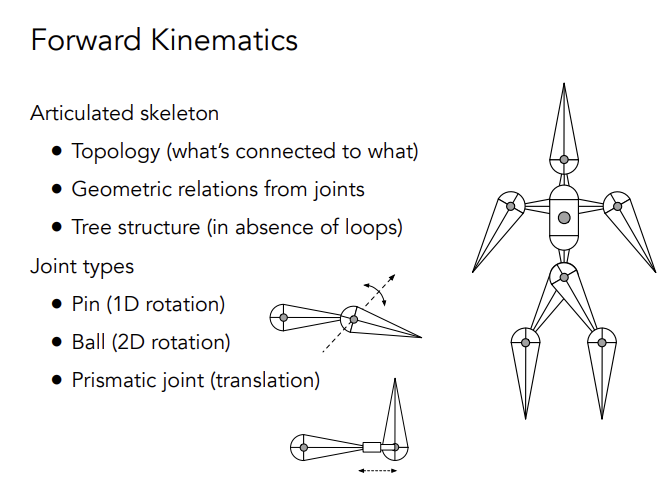
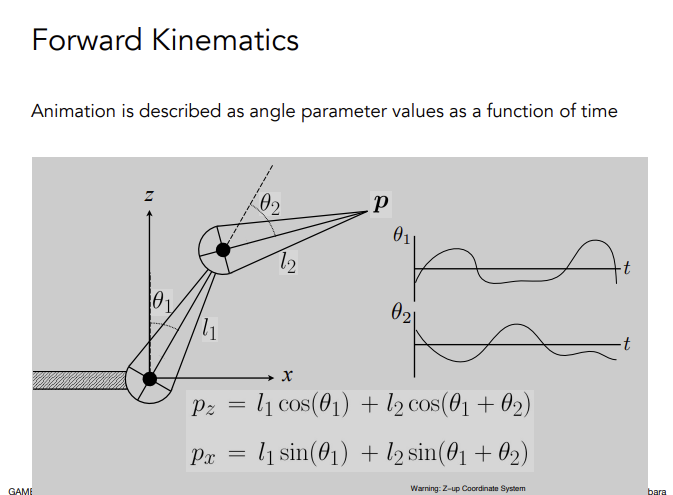
Forwardd Kinematics
正向运动学是通过定义一些可活动关节(如铰链),通过计算来控制末端的点的运动
 |
 |
|---|
但对于艺术家而言习惯控制末端的点
Inverse Kinematics

但存在如下难点:
- 关节到达一个点有多种方法
- 有可能不存在解
要优化解的选择涉及到深度学习(随机化算法、梯度下降等)



