Games202 Real-time Shadows
Real-time Shadows
Shadow mapping
光和相机都能看到的点 = 不在阴影里的点
从光源看,记录深度
从摄像机看,计算点到light的深度并和从light看这个点的深度对比,相等则无阴影,不相等则有遮挡

自遮挡
- shadow map 上每个采样点都代表一块范围的深度值,第二趟和第一趟比较深度时不一致,产生阴影。

解决:
- 添加一个偏移值 bias,在一定误差内认为相等。
问题:

解决:
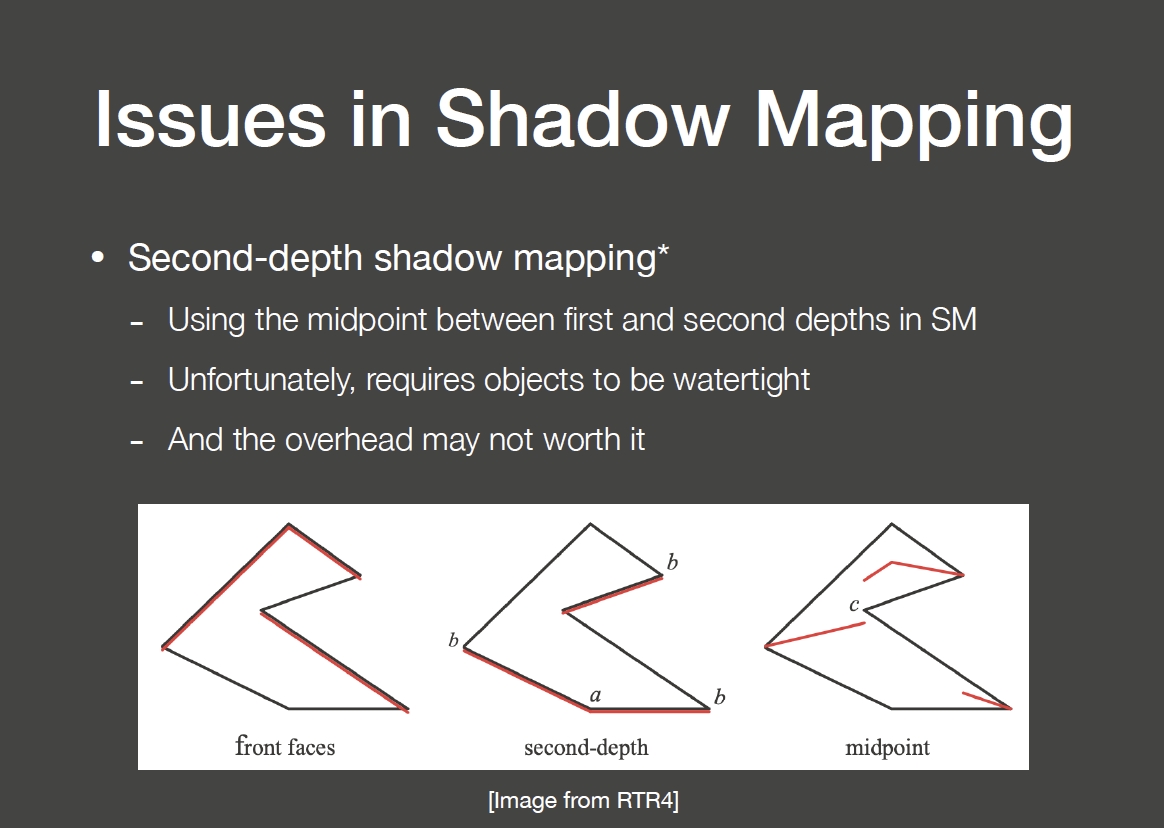
锯齿

硬阴影

解决锯齿问题
Percentage Closer Filtering(PCF)

有锯齿的阴影每个点非 0 即 1,要么是阴影要么不是。
PCF 对每个 shading point,在 shadow map 上找其周边(例如3*3)的点,最后取平均值,这样某个地方的值就是 0-1 之间。
实现软阴影
Percentage Closer Soft Shadow(PCSS)
PCF 中取一个较大的 Filter,就可以实现软阴影。但 Filter 的尺寸应该是自适应的。有点地方硬阴影,有些地方软阴影。

Filter 的 size 取决于 Light 的大小和距离。
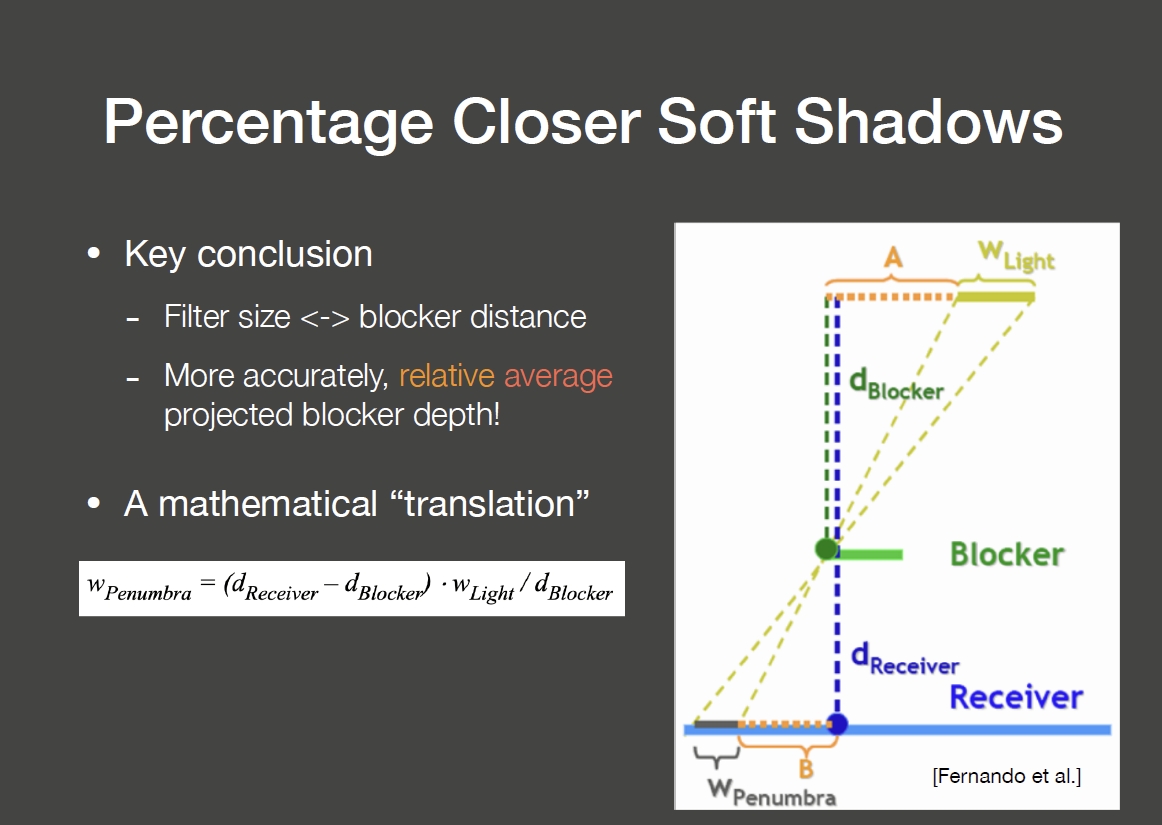
PCSS的具体步骤如下:
- 首先依据着色点选择一块范围,对 Shadow Map 做一次局部深度测试,找到范围内的 blocker 并计算其平均深度(计算平均深度的目的是减小遮挡物自身的几何影响,避免漏光)
- 得到 d_blocker 后代入公式计算滤波范围, d_blocker 越小, d_receiver - d_blocker 越大,卷积核越大,得到的阴影就越软
- 重新进行深度测试,继续完成PCF的过程

PCSS 可以通过减少采样来得到结果,例如 64*64 中采样三个点,但是会产生噪声。然而目前对于噪声的处理比较成熟,因此通常使用 PCSS。
VSSM
Variance Soft Shadow Mapping
PCSS 的 step1 和 step3 需要看一个区域的所有像素点,耗费时间。
VSSM 通过几种方法加速 step1 和step3
求平均
- MipMap
- Summed Area Tables(SAT)
求方差
- $Var(x) = E(x^2) - E^2(x)$
只需要额外一张 shadow map 存储 $E(x^2)$,也可以放在两个 RGB 通道中。
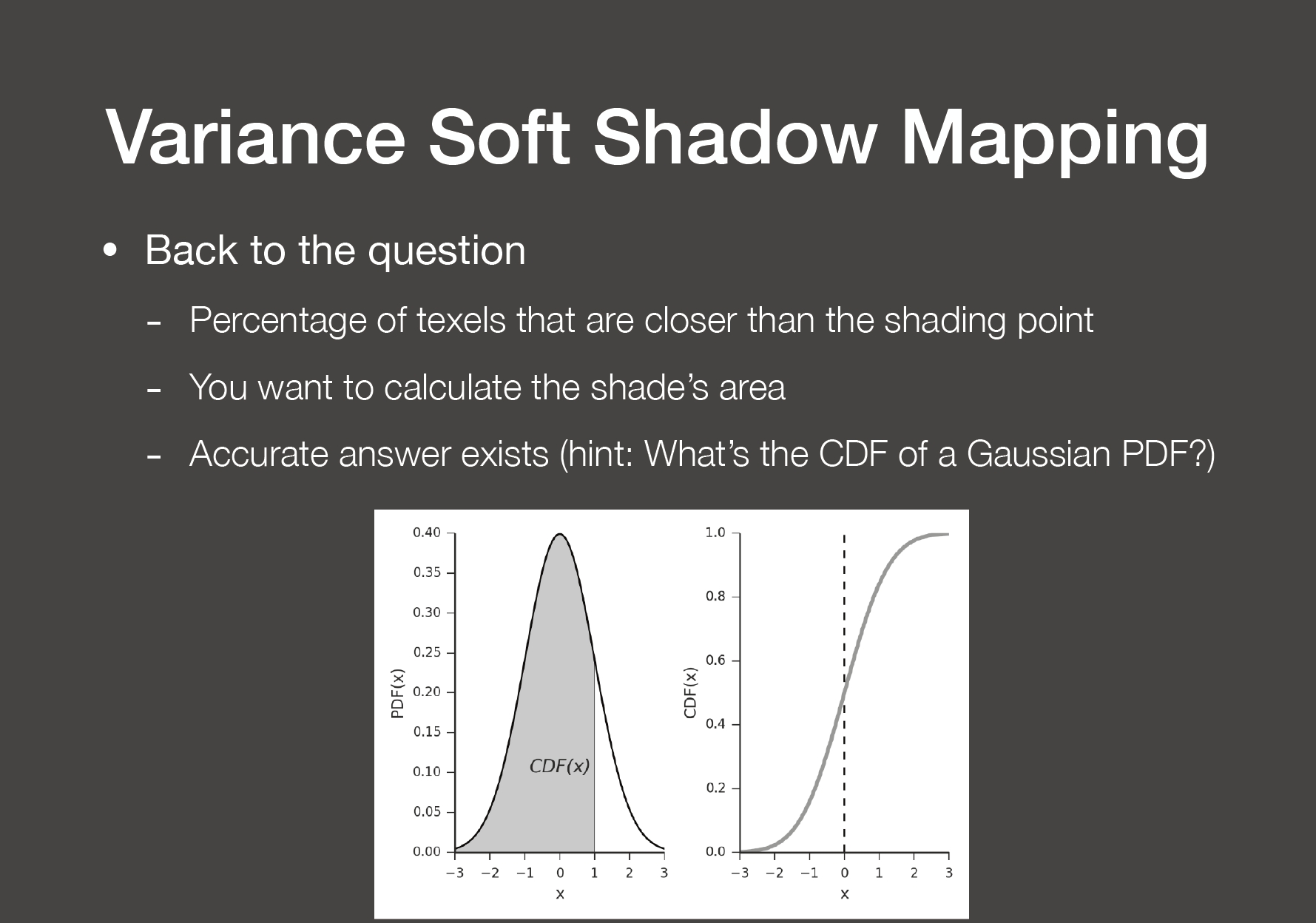
知道方差和均值可以用高斯正态分布来计算有多少比例的像素点比 shading point 近。
可以通过数值解或者查表来解,但还是比较慢,采用近似。
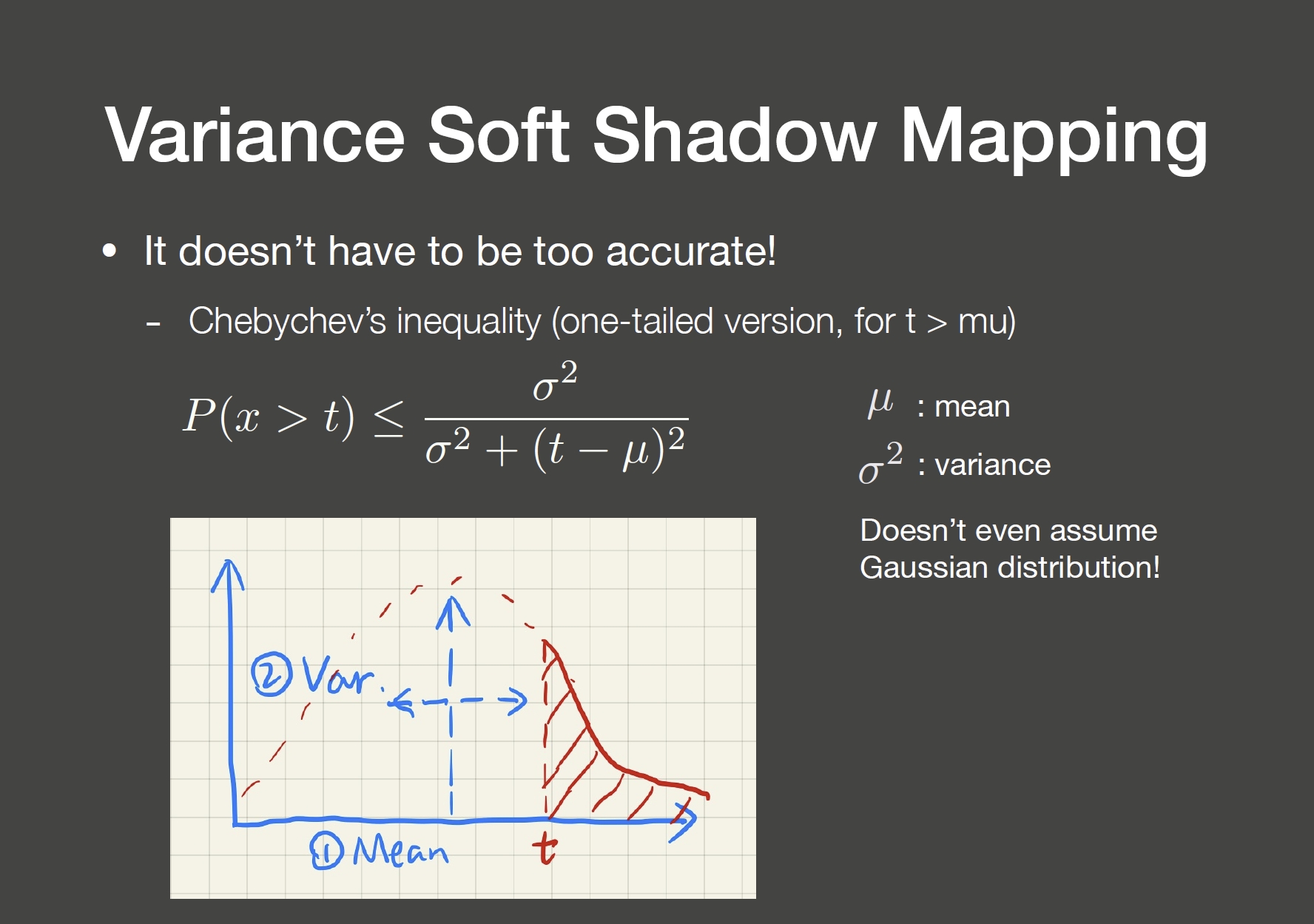
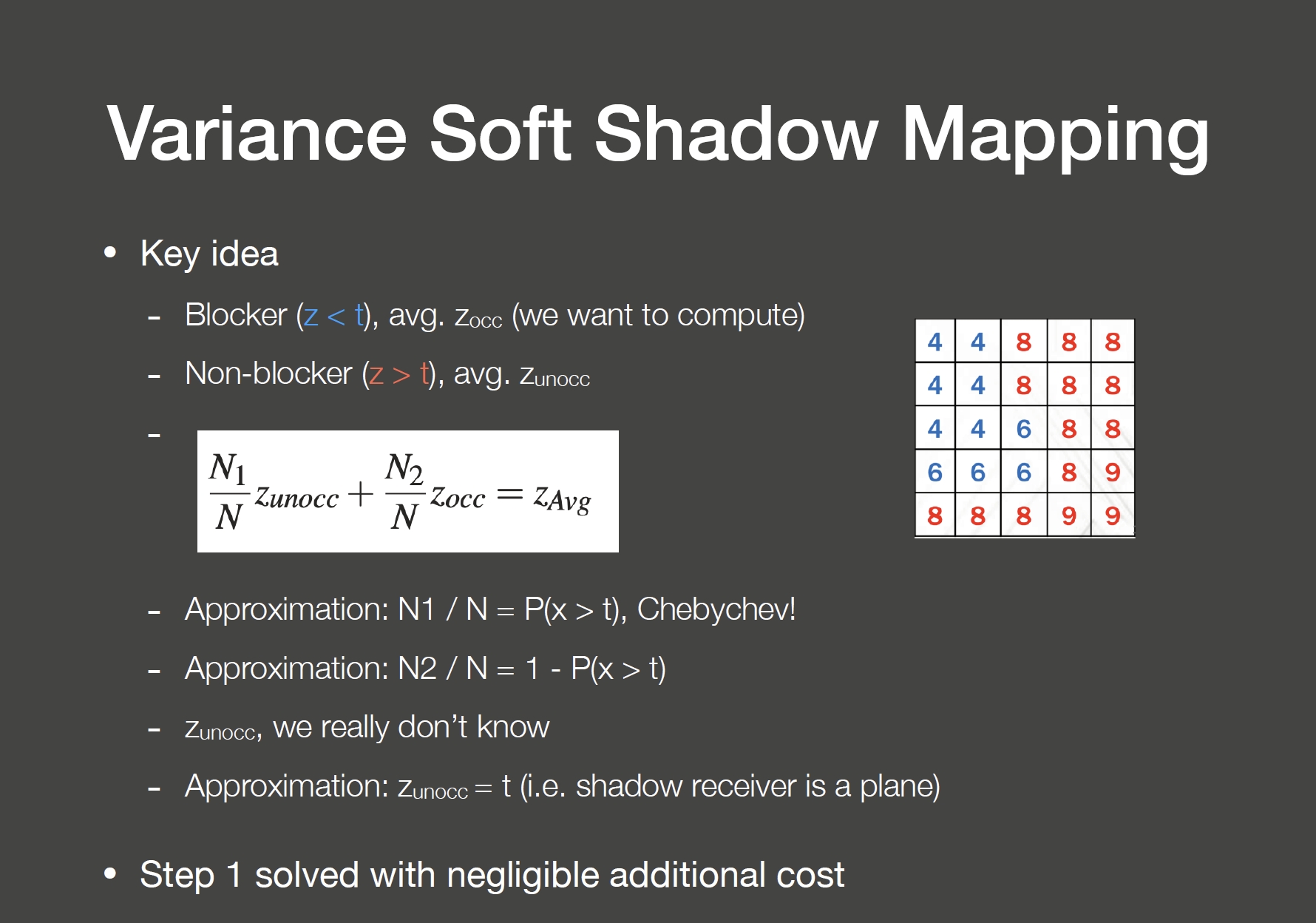
- N1:遮挡物格子数
- N2:非遮挡物格子数
- Z:深度
N1/N 可以用 Chebychev 不等式估计,非遮挡物平均深度假设都在同一平面全部相等。
SAT
Summed Area Tables

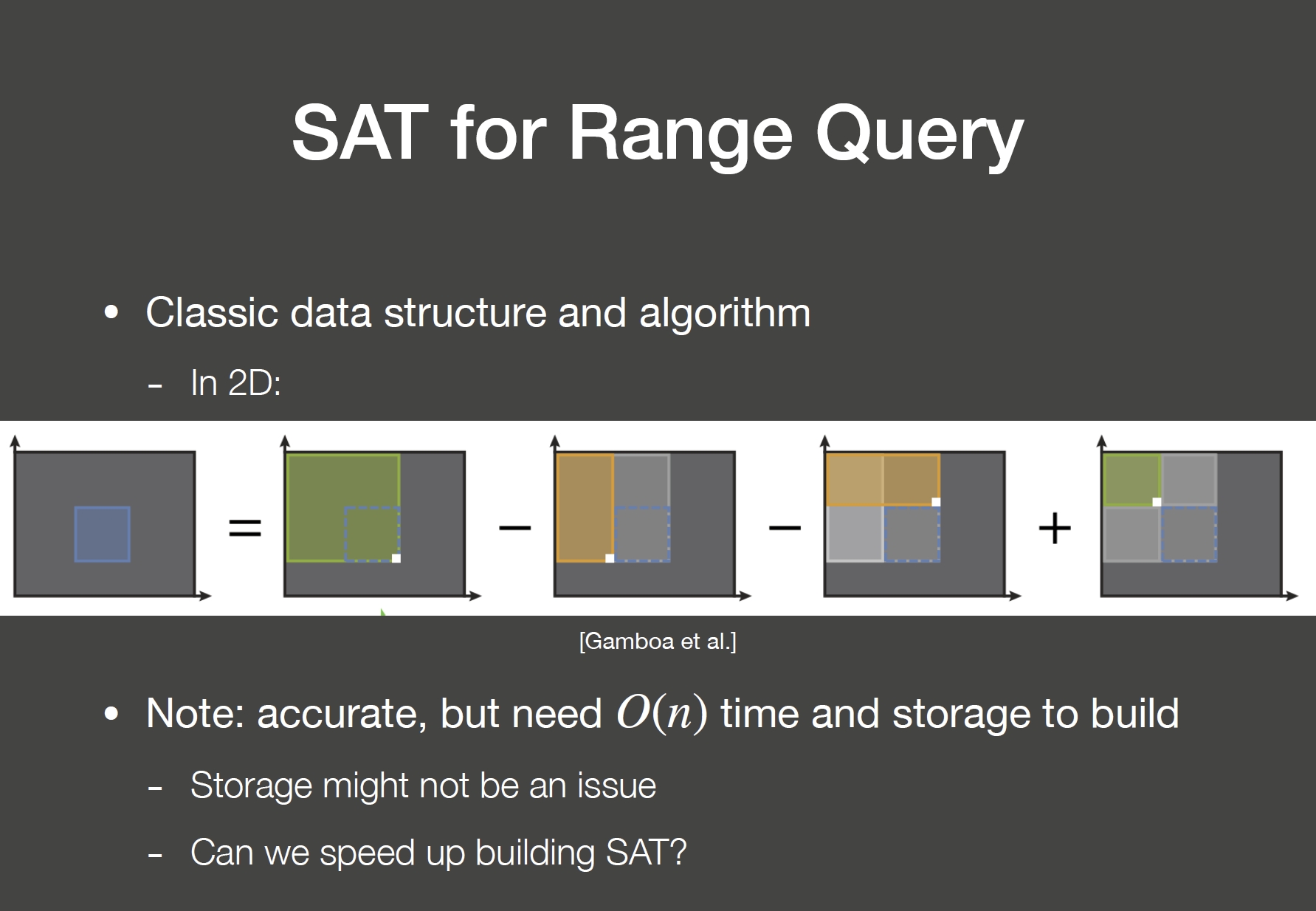
MSM
Moment Shadow Mapping
VSSM 中当一些环境简单的情况下,遮挡物的分布不会近似高斯分布。

VSSM 用 $Var(x) = E(x^2) - E^2(x)$ 两阶,但用更高的阶可以更接近。

SDF
Distance Field of Shadow
对每个点记录离物体最近的距离

Ray Marching
一般用于 Ray Tracing,光线可以行进 SDF(p) 的距离。

也可以用于生成软阴影,一个面光源和一个点生成一个锥形,通过最小的 SDF 来计算遮挡的比例,从而得到点的遮挡度。

遮挡比例需要用 arcsin 来计算,可以简化,k值可以控制阴影软硬程度。

三维中的距离场的可视化:

优缺点:
快,高质量,但是需要提前计算,需要存储,且不适用于形变物体。


