Games202 Real-time Environment Mapping
Real-time Environment Mapping


渲染方程:渲染方程
需要一些快速的方法解这个方程

在 g(x) 积分域小或 g(x) 平滑时可以取约等
另一种理解:

理解成 f(x) 在 g(x) 积分域下的平均 * g(x) 的积分
Split Sum
将渲染方程拆分

先算第一步
在算之前可以预处理(类似于 MipMap )

例如以半径1,2,4,8大小的滤波核进行处理。
某个区域内的积分就是这一区域内的和,可以从之前经过滤波的图中直接取到。
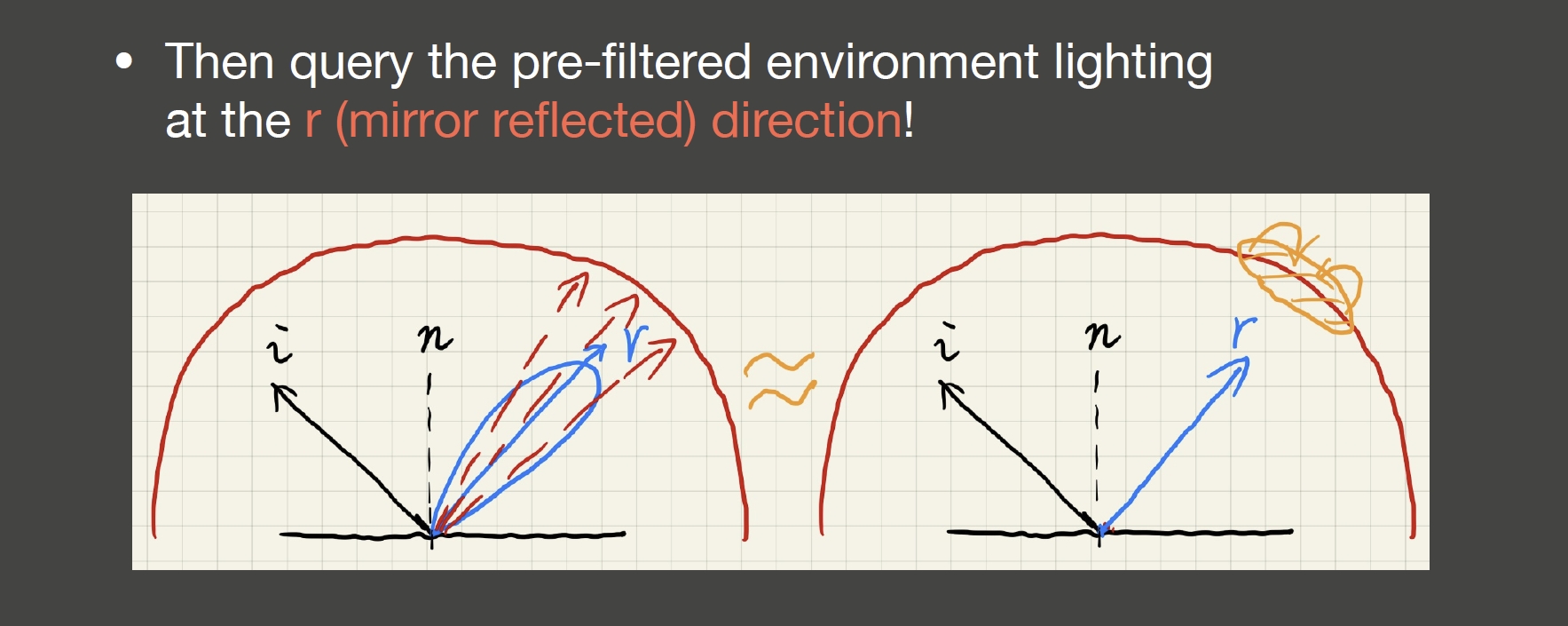
接着是第二步
右边这部分参数很多,不适用于预计算。

以为微表面 BRDF 为例
对于 Fresnel 和 NDF 的近似:

由此变为 3 维的积分,有 3 个参数 R0,θ,α
NDF:法线分布
α:粗糙度,第二个图像的胖瘦
θ:入射角
R0:基础反射率,颜色
n:η,折射率,跟介质有关
R0可以拆到积分外面,简化成 2 维

fr/F 后 fr 只用考虑 NDF 项,即 Roughness
积分只有两个参数 θ 和 Roughness,存成 2 维数组,相当于纹理

PRT
Precomputed radiance transfer

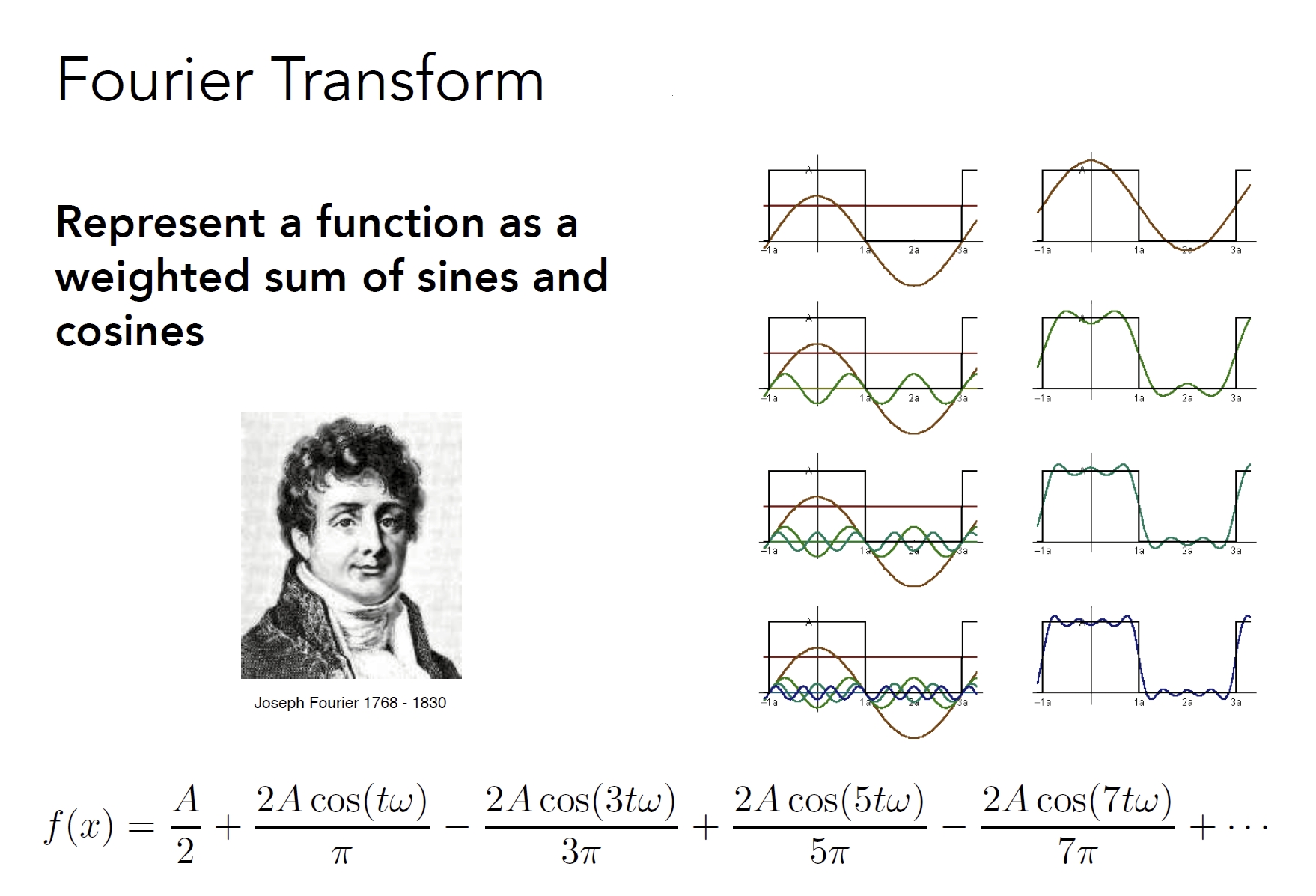
傅里叶变换
任意函数可以拆分为多个基函数
空域的卷积等于频域上的乘积
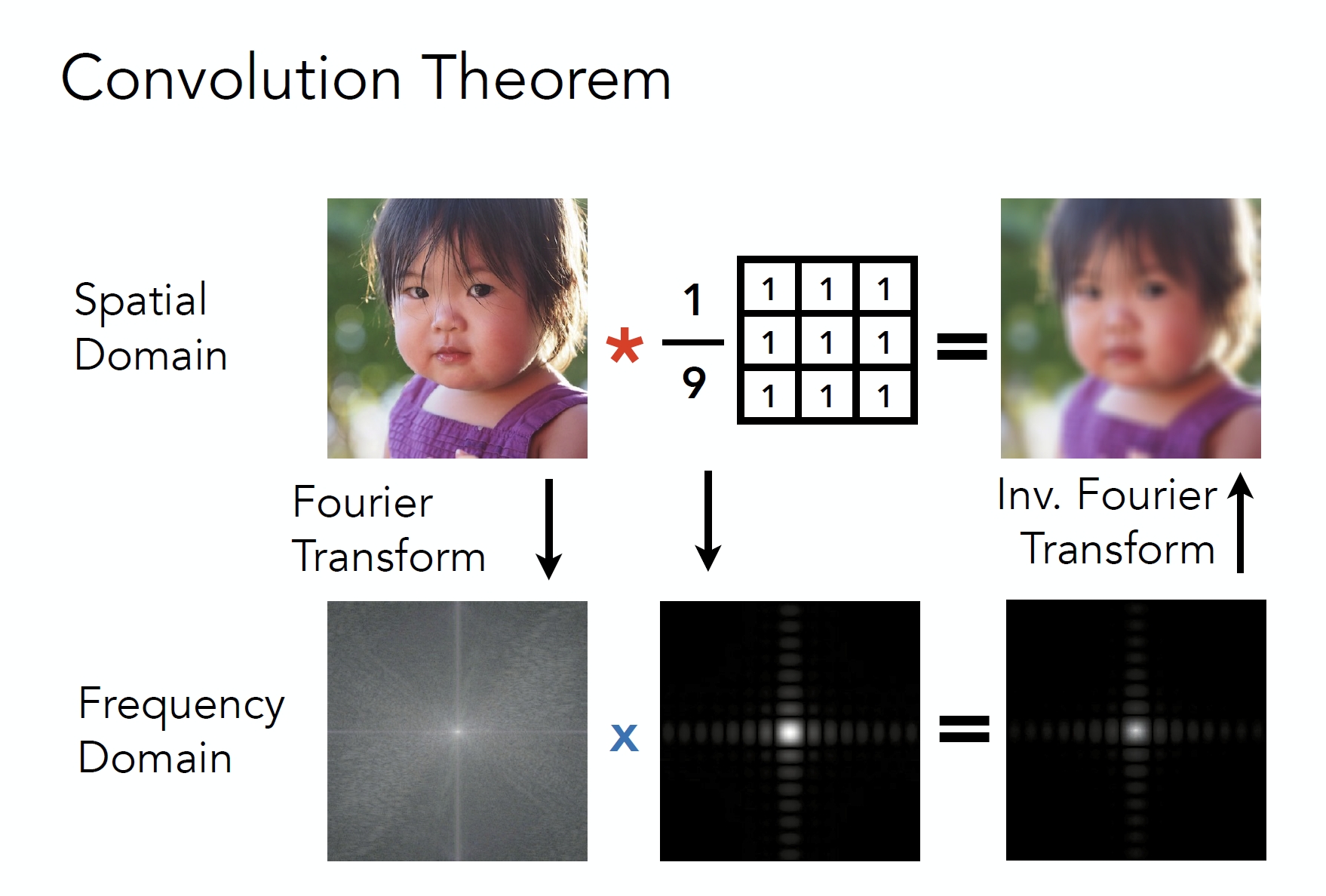
两个函数的乘积的积分可以理解成卷积
这个积分结果的频率由两个函数中各自的最低频决定

Spherical Harmonics
球面谐波函数
二维的基函数

其次这里涉及到一个投影的操作
给定任何一个球面函数,如果我们想把它展开成某阶的一系列球谐函数的基函数,那么其中某个基函数的系数 ci 就等于把这个函数 f 和这个基函数做乘积再积分得到的结果,这就是投影 Projection 操作
这里和一个我们熟知的操作类似,假设我们三维空间有一个向量,我们需要用 (x,y,z) 坐标表示它,那么 xyz 的值是这个三维向量在各个坐标轴上的投影
球谐函数的各个基函数就可以理解为三维空间的各个坐标轴,而想要表示的函数自然就是那个三维空间的向量
其次,三维空间中我们的投影变成了乘积的积分而不是点乘。事实上,乘积再积分的操作本质上就是点乘,也就是dot操作。其次我们想三维空间的三个坐标轴互相投影为0,也就是说它们是正交的/互相垂直的,而事实上球谐函数的各个基函数也互相垂直。

不考虑 Shadow 的 PRT
对于 Diffuse 的 BRDF,求 Environment 的 Shading 时,要把 BRDF 和环境光的函数相乘然后半球积分,这正是我们之前提到的**乘积再积分 (product integral) **的操作。因为 BRDF 是低频的,我们可以把 BRDF 看作一个低通滤波器,只需要0,1,2阶就足够了(更高阶的系数基本接近于 0,可以舍去)
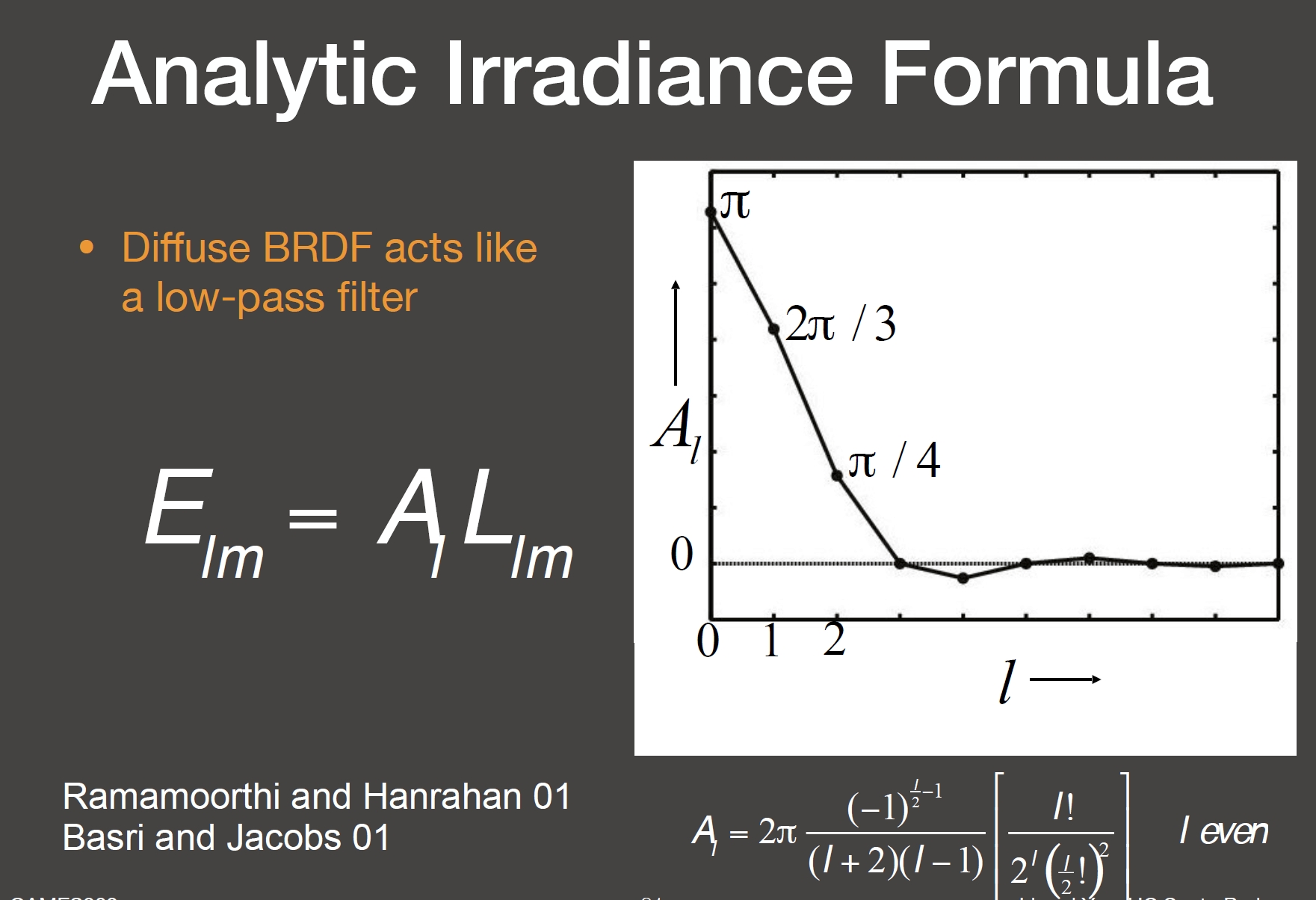
回到我们前面的 product integral 操作上,乘积再积分的结果的频率取决于低频部分,由也就是说,即使外界环境光再复杂,遇到了 Diffuse 的 BRDF,物体的表面也不会呈现出很复杂的杠光照,这也符合我们的常识。因此,用前 3 阶的 SH 描述光照得到的结果和正确的结果基本一致。

考虑 Shadow 的 PRT
我们重新分析一下渲染方程,它包括 Lighting 项,Visibility 项,BRDF 项,它们三个都可以表示为一个球面函数,那最终结果的颜色 (带着Shadow) 自然就是它们三项的对应值/像素相乘了

PRT的思想是,我们先假设场景中只有 Lighting 项可以变,如光照类型/反向,其它条件都不变。这样渲染方程就被我们拆成了两部分,一项我们叫 Lighting,另一项我们叫它 light transport。其次,在预计算的时候,PRT 把 Lighting 项拆成了一系列 SH 基函数。又因为我们前面提到,场景中除了光照其他条件都不变,那么显然 light transport 项也不会发生变化,它相当于着色点自身的性质,既然light transport 不变,那我们就可以在渲染之前把它预计算好。

简化为点乘

因为 Diffuse 的 BRDF 是一个常数,所以我们可以把它从积分中提出,这里我们写作ρ。其次用我们前面提到的球谐函数可以把 Li 项用一系列基函数表示变成求和项。然后交换积分与求和的顺序(图形学中大多数情况都可以调换积分和求和的顺序),此时基函数的系数 li 也可以从积分中提出。此时我们可以看到右边划红线的部分变成了,Visibility 项和 cos 项的乘积也就是 light transport 项,再乘一个基函数然后积分,这不就是 Light transport 项在 SH 各个基函数上的投影吗。
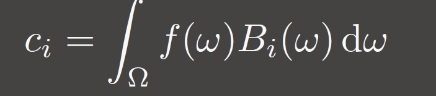
显然,上图划红线的部分直接可以预计算得到,最后组成一个表格存储计算的结果。于是最终的形式就变成一个点乘,就可以计算出 Diffuse 下的环境光照并且带有 Shadow。
当然,我们前面提到,我们只假设了光源可以改变,其它场景条件不变,那么 Visibilty 项不能变,着色点周围的遮挡关系就不能改变。
其次因为光源也做了预计算,如果要更换光源,我们要对不同的想要使用的光源都进行预计算。那么如果光源可以旋转呢?这里可以用球谐函数的一个很好的可以旋转的性质解决。

PRT 其他理解
可以将基函数 Bi 想象成光源,提前进行预计算。最终计算某个环境光下的 shading 时,就用该环境光展开的 Bi (已经预计算过)累加。

也可以换一种计算方法
只有当 p==q 时才有意义,因为球谐函数具有正交性。与之前的结果是等价的。

PRT For Glossy
对于 Glossy 的物体,BRDF 无法当作常数,BRDF需要两个参数入射角度和出射角度,即 4 维。
之前对于 Diffuse 物体,假设 n 阶展开,每个像素只用存储 $n^2$ 个值,相当于存储每个 Light 的展开项对这个点的影响。
对于 Glossy 物体,像素点要存 $n^2*n^2$ 的值。

PRT 的局限
- 球谐函数只适合于描述低频的函数,描述高频要用很高阶的基函数
- 因为预计算,所以只适用于静态场景。材质,场景都不能发生改变
Wavelet
小波变换(类似于 SH 的基函数)
可以表示全频段
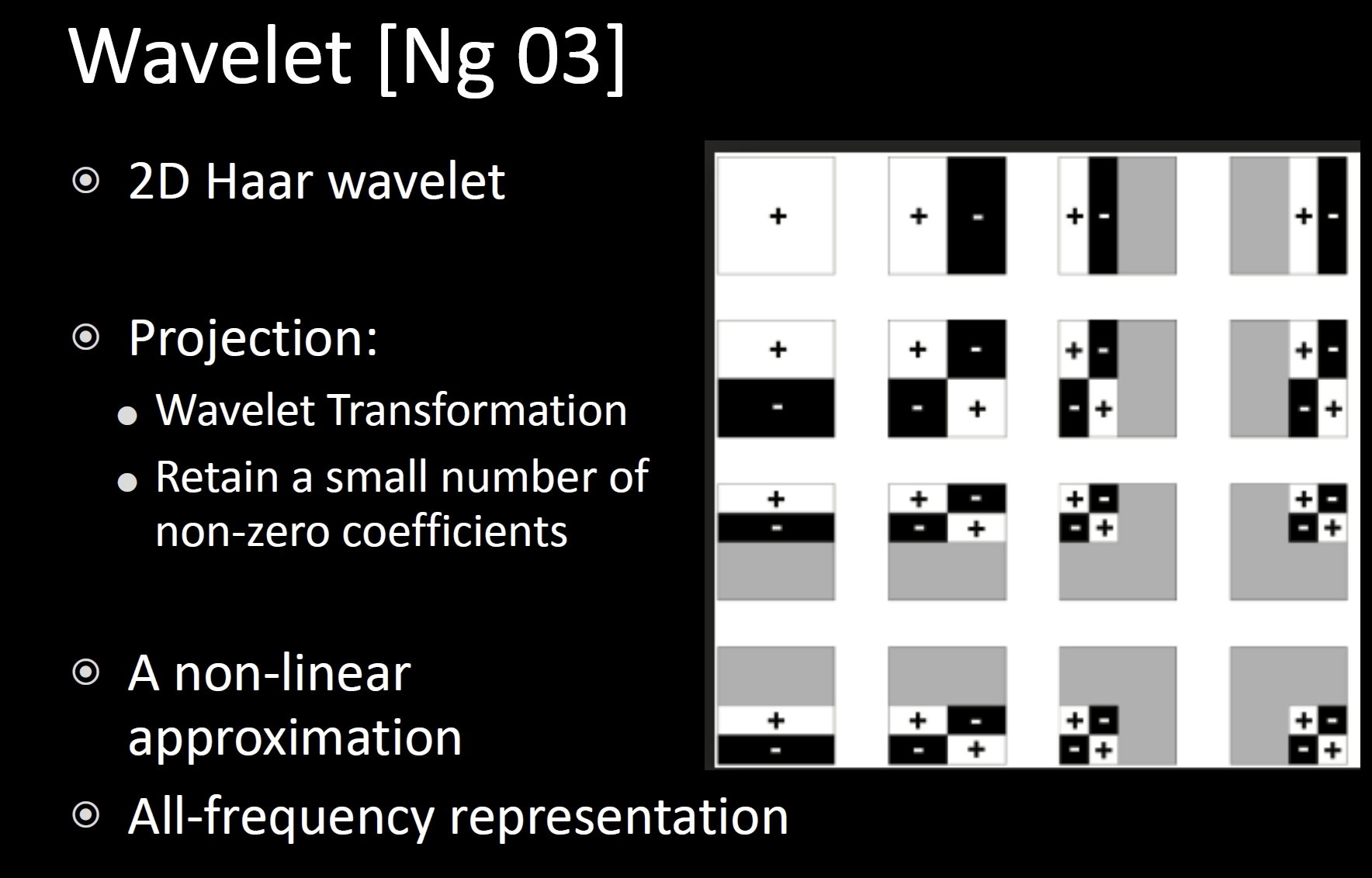
但是不能旋转光照


