线性回归模型

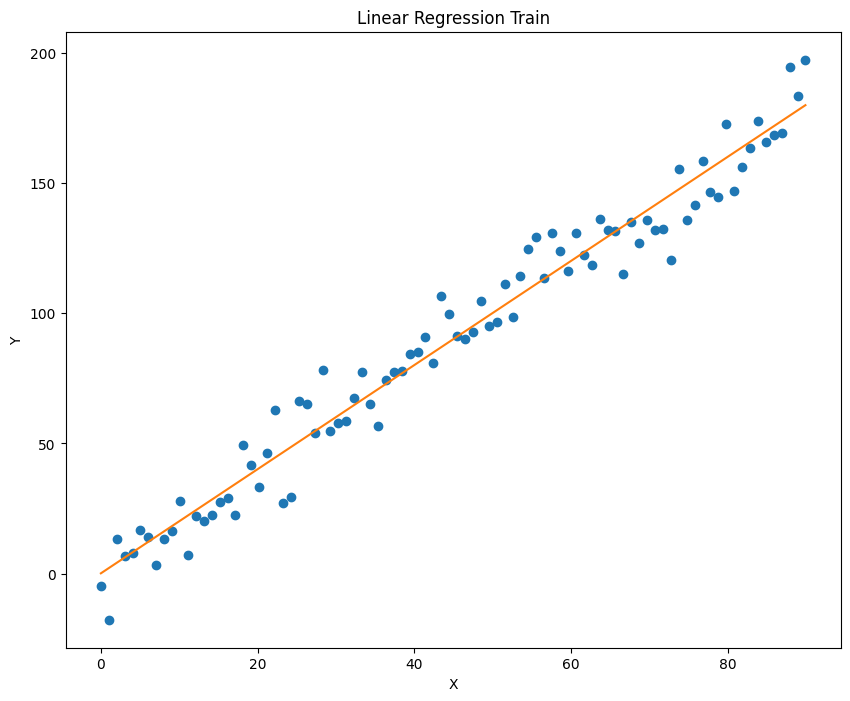
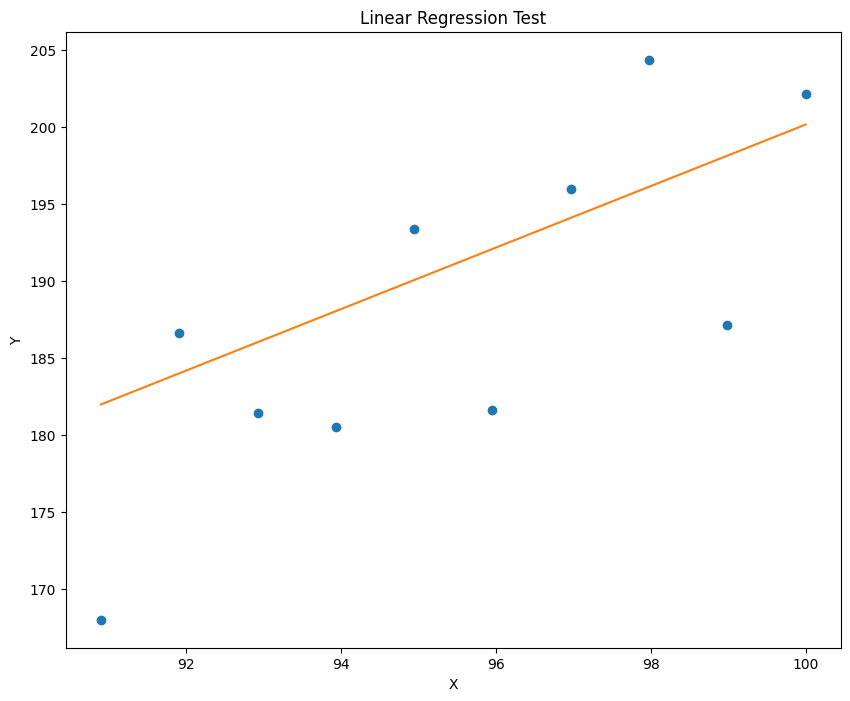
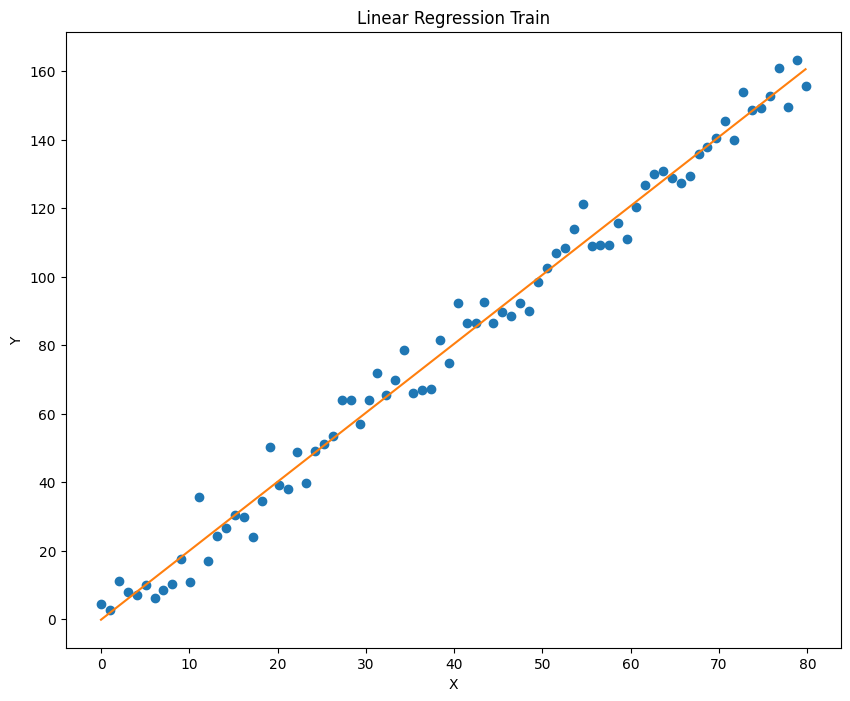
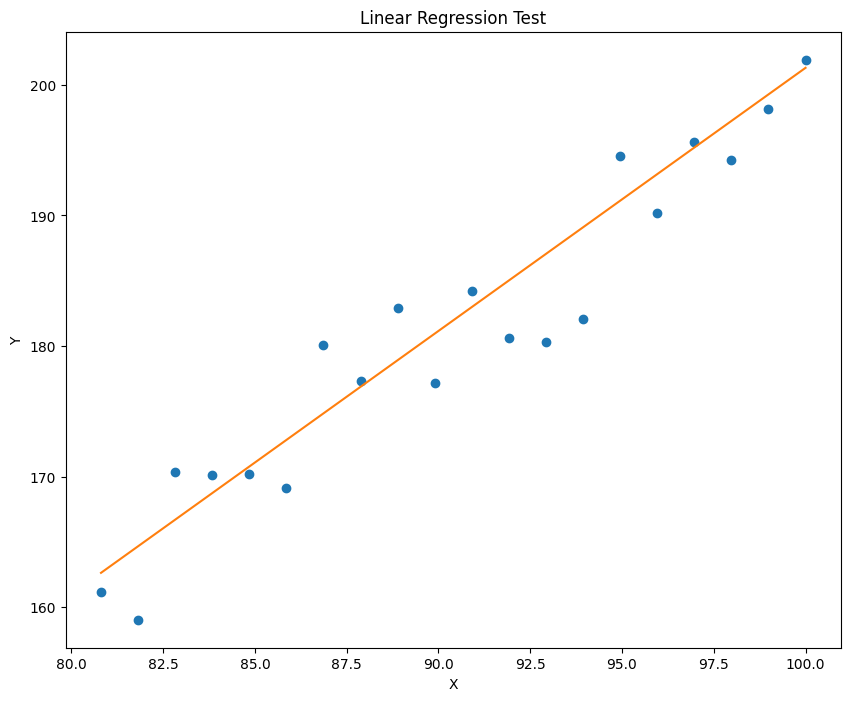
  • 已知模型 y=ax+b，输入浮点数 a,b 并生成加噪后的数据，再利用梯度下降算法迭代得到 a,b。利用的到模型对数据拟合并进行预测，记录误差，并绘制出拟合效果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import torch
import numpy as np
import matplotlib.pyplot as plt


def generate_noisy_data(a, b, noise_stddev=10):
    a = float(a)
    b = float(b)
    x = torch.linspace(0, 100, steps=100, dtype=torch.float32)
    rand = torch.randn(100) * noise_stddev
    b = b * torch.ones_like(x)
    y = a * x + b + rand
    train_x = x[0:90]
    test_x = x[90:100]
    train_y = y[0:90]
    test_y = y[90:100]
    return train_x, test_x, train_y, test_y


def linear_regression(train_x, train_y, num_iterations=10000, learning_rate=0.0001):
    
    # requires_grad = True 执行后，PyTorch会跟踪这些参数的操作，并在计算图中建立依赖关系。
    # 当调用 loss.backward() 时，PyTorch会根据这个计算图计算损失相对于所有具有 requires_grad=True 的参数的梯度。
    
    a = torch.rand(1, requires_grad=True)
    b = torch.rand(1, requires_grad=True)

    for i in range(num_iterations):
        pred = a.expand_as(train_x) * train_x + b.expand_as(train_x)
        loss = torch.mean((pred - train_y) ** 2)
        if i % 1000 == 0:
            print("loss:", loss.data)
        loss.backward()
        a.data = a.data - learning_rate * a.grad.data
        b.data = b.data - learning_rate * b.grad.data
        a.grad.data.zero_()
        b.grad.data.zero_()

    return a, b


def plot_fit(train_x, train_y, a, b, title="Linear Regression"):
    plt.figure(figsize=(10, 8))
    plt.plot(train_x.data.numpy(), train_y.data.numpy(), 'o')
    plt.plot(train_x.data.numpy(), (a * train_x + b).data.numpy())
    plt.title(title)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()


def main():
    (a, b) = (2, 1)

    num_iterations = 10000
    learning_rate = 0.0001

    train_x, test_x, train_y, test_y = generate_noisy_data(a, b)
    a_hat, b_hat = linear_regression(train_x, train_y, num_iterations, learning_rate)
    plot_fit(train_x, train_y, a_hat, b_hat, title="Linear Regression Train")
    plot_fit(test_x, test_y, a_hat, b_hat, title="Linear Regression Test")


if __name__ == "__main__":
    main()

输出：

loss: tensor(3678.7781)
loss: tensor(99.0996)
loss: tensor(99.0956)
loss: tensor(99.0920)
loss: tensor(99.0887)
loss: tensor(99.0858)
loss: tensor(99.0831)
loss: tensor(99.0807)
loss: tensor(99.0786)
loss: tensor(99.0766)

png

png

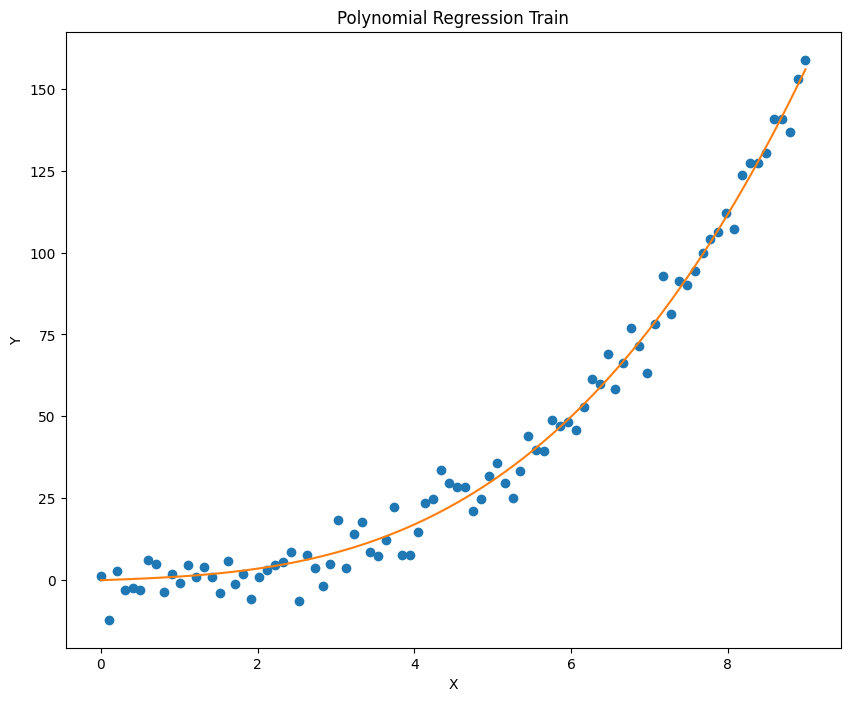
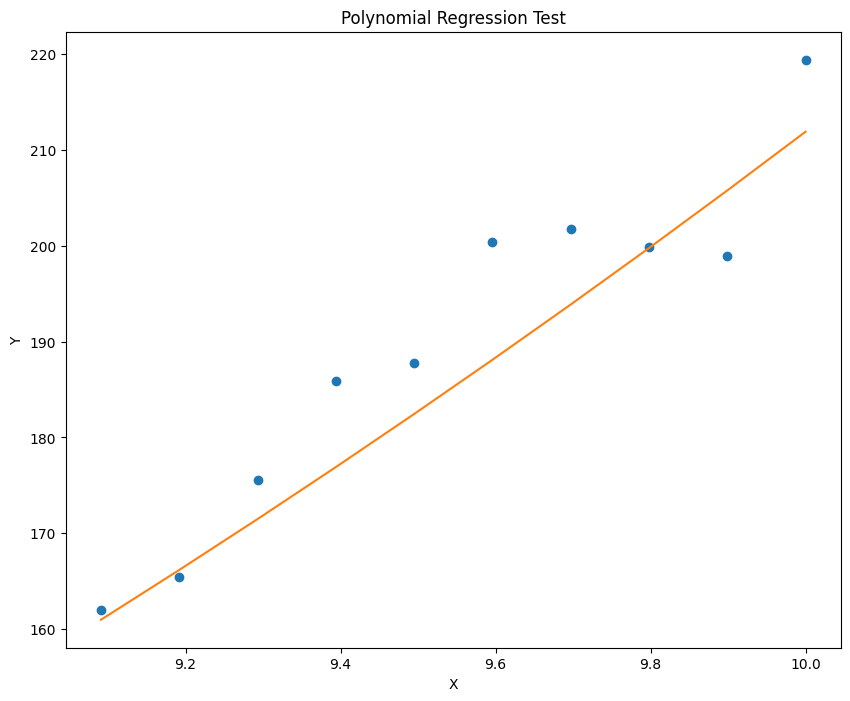
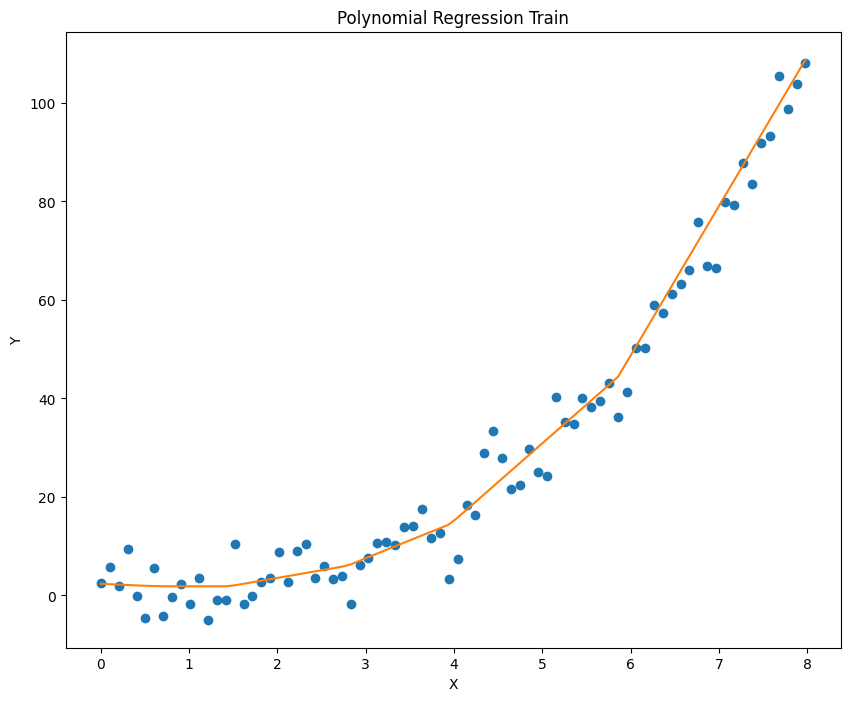
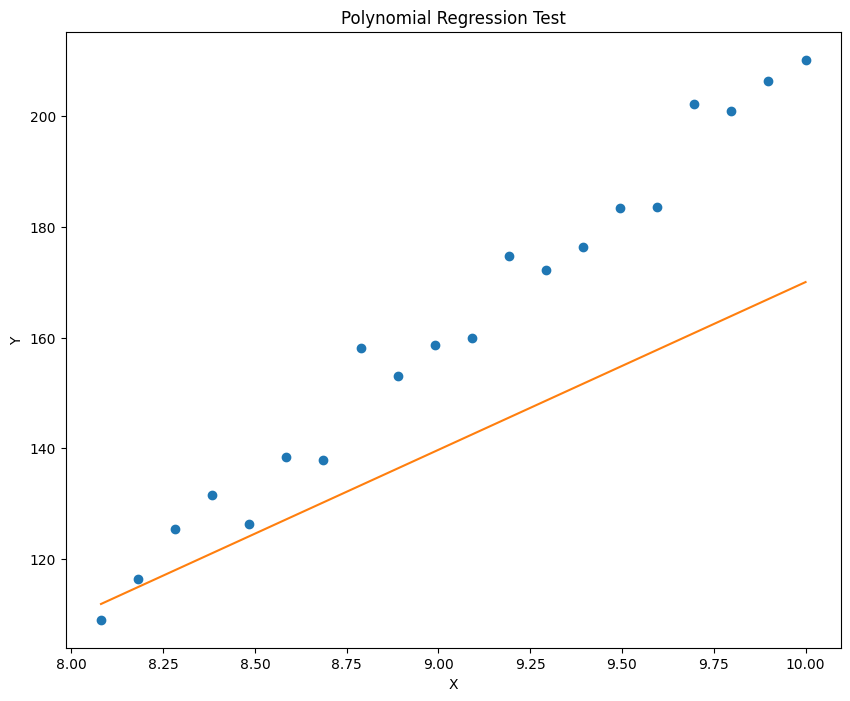
  • 已知模型 y=a*x^3 + b*x^2 + c*x + d，输入浮点数 a,b,c,d 并生成加噪后的数据，再利用梯度下降算法迭代得到 a,b,c,d。利用的到模型对数据拟合并进行预测，记录误差，并绘制出拟合效果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import torch
import numpy as np
import matplotlib.pyplot as plt


def generate_noisy_data(a, b, c, d, noise_stddev=5):
    a = float(a)
    b = float(b)
    c = float(c)
    d = float(d)
    x = torch.linspace(0, 10, steps=100, dtype=torch.float32)
    rand = torch.randn(100) * noise_stddev
    d = d * torch.ones_like(x)
    y = a * x ** 3 + b * x ** 2 + c * x + d + rand
    train_x = x[0:90]
    test_x = x[90:100]
    train_y = y[0:90]
    test_y = y[90:100]
    return train_x, test_x, train_y, test_y


def polynomial_regression(train_x, train_y, num_iterations=10000, learning_rate=0.0001):
    a = torch.rand(1, requires_grad=True)
    b = torch.rand(1, requires_grad=True)
    c = torch.rand(1, requires_grad=True)
    d = torch.rand(1, requires_grad=True)

    for i in range(num_iterations):
        pred = a.expand_as(train_x) * train_x ** 3 + b.expand_as(train_x) * train_x ** 2 + c.expand_as(
            train_x) * train_x + d.expand_as(train_x)
        loss = torch.mean((pred - train_y) ** 2)
        if i % 1000 == 0:
            print("loss:", loss.data)
        loss.backward()
        a.data = a.data - learning_rate * a.grad.data
        b.data = b.data - learning_rate * b.grad.data
        c.data = c.data - learning_rate * c.grad.data
        d.data = d.data - learning_rate * d.grad.data
        a.grad.data.zero_()
        b.grad.data.zero_()
        c.grad.data.zero_()
        d.grad.data.zero_()

    return a, b, c, d


def plot_fit(train_x, train_y, a, b, c, d, title="Polynomial Regression"):
    plt.figure(figsize=(10, 8))
    plt.plot(train_x.data.numpy(), train_y.data.numpy(), 'o')
    plt.plot(train_x.data.numpy(), (a * train_x ** 3 + b * train_x ** 2 + c * train_x + d).data.numpy())
    plt.title(title)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()


def main():
    (a, b, c, d) = (0.2, 0.15, 0.1, 0.05)

    num_iterations = 10000
    learning_rate = 0.00001

    train_x, test_x, train_y, test_y = generate_noisy_data(a, b, c, d)
    a_hat, b_hat, c_hat, d_hat = polynomial_regression(train_x, train_y, num_iterations, learning_rate)
    plot_fit(train_x, train_y, a_hat, b_hat, c_hat, d_hat, title="Polynomial Regression Train")
    plot_fit(test_x, test_y, a_hat, b_hat, c_hat, d_hat, title="Polynomial Regression Test")


if __name__ == "__main__":
    main()

输出：

loss: tensor(174.3713)
loss: tensor(27.0408)
loss: tensor(26.6397)
loss: tensor(26.5540)
loss: tensor(26.5305)
loss: tensor(26.5192)
loss: tensor(26.5106)
loss: tensor(26.5025)
loss: tensor(26.4947)
loss: tensor(26.4870)

png

png

神经网络模型

  • y = ax + b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.nn.functional as F


def generate_noisy_data(a, b, noise_stddev=5):
    a = float(a)
    b = float(b)

    x = torch.linspace(0, 100, steps=100, dtype=torch.float32)
    rand = torch.randn(100) * noise_stddev
    y = a * x + b + rand
    train_x = x[0:80]
    test_x = x[80:100]
    train_y = y[0:80]
    test_y = y[80:100]
    return train_x, test_x, train_y, test_y


class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.out = nn.Linear(1, 1)

    def forward(self, x):
        x = self.out(x)
        return x


def neural_network(net, loss_fn, opt, train_x, train_y, num_iterations=10000):
    for i in range(num_iterations):
        pred = net(train_x.view(-1, 1))
        loss = loss_fn(pred, train_y.view(-1, 1))
        if i % 2000 == 0:
            print("loss:", loss.data)

        opt.zero_grad()
        loss.backward()
        opt.step()
        
    # pred：通过神经网络进行前向传播，得到模型对输入数据的预测值。
    # loss：使用损失函数计算预测值与真实标签之间的损失，平均平方差 loss_fn = torch.nn.MSELoss()
    # opt：使用的是随机梯度下降优化器 (torch.optim.SGD)，它根据损失函数的梯度来更新模型的权重，使得损失逐渐减小。
    # opt.zero_grad()：清零之前的梯度，因为PyTorch默认会累积梯度。
    # loss.backward()：通过反向传播计算损失相对于模型参数的梯度。
    # opt.step()：根据梯度更新模型参数，实现梯度下降。
    # .view(-1, 1)确保数据是二维的 例如：[ [1],[2],[3] ]

def plot_fit(net, train_x, train_y, title="Polynomial Regression"):
    plt.figure(figsize=(10, 8))
    plt.plot(train_x.data.numpy(), train_y.data.numpy(), 'o')
    plt.plot(train_x.data.numpy(), net(train_x.view(-1, 1)).data.numpy())
    plt.title(title)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()


def main():
    (a, b) = (2, 1)

    train_x, test_x, train_y, test_y = generate_noisy_data(a, b)
    net = Model()
    loss_fn = torch.nn.MSELoss();
    opt = torch.optim.SGD(net.parameters(), lr=0.0001)
    num_iterations = 10000

    neural_network(net, loss_fn, opt, train_x, train_y, num_iterations)
    plot_fit(net, train_x, train_y, title="Linear Regression Train")
    plot_fit(net, test_x, test_y, title="Linear Regression Test")
    print(net(test_x.view(-1, 1)))


if __name__ == "__main__":
    main()

输出：

loss: tensor(4889.4863)
loss: tensor(28.3156)
loss: tensor(28.3152)
loss: tensor(28.3149)
loss: tensor(28.3146)

png

png

tensor([[162.6327],
        [164.6684],
        [166.7040],
        [168.7396],
        [170.7753],
        [172.8109],
        [174.8465],
        [176.8822],
        [178.9178],
        [180.9534],
        [182.9891],
        [185.0247],
        [187.0603],
        [189.0960],
        [191.1316],
        [193.1672],
        [195.2029],
        [197.2385],
        [199.2741],
        [201.3098]], grad_fn=<AddmmBackward0>)
  • y=a*x^3 + b*x^2 + c*x + d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.nn.functional as F


def generate_noisy_data(a, b, c, d, noise_stddev=5):
    a = float(a)
    b = float(b)
    c = float(c)
    d = float(d)

    x = torch.linspace(0, 10, steps=100, dtype=torch.float32)
    rand = torch.randn(100) * noise_stddev
    y = a * x ** 3 + b * x ** 2 + c * x + d + rand
    train_x = x[0:80]
    test_x = x[80:100]
    train_y = y[0:80]
    test_y = y[80:100]
    return train_x, test_x, train_y, test_y


class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden1 = nn.Linear(1, 5)
        self.hidden2 = nn.Linear(5, 10)
        self.hidden3 = nn.Linear(10, 5)
        self.out = nn.Linear(5, 1)

    def forward(self, x):
        x = self.hidden1(x)
        x = F.relu(x)
        x = self.hidden2(x)
        x = F.relu(x)
        x = self.hidden3(x)
        x = F.relu(x)
        x = self.out(x)
        return x


def neural_network(net, loss_fn, opt, train_x, train_y, num_iterations=10000):
    for i in range(num_iterations):
        pred = net(train_x.view(-1, 1))
        loss = loss_fn(pred, train_y.view(-1, 1))
        if i % 2000 == 0:
            print("loss:", loss.data)

        opt.zero_grad()
        loss.backward()
        opt.step()


def plot_fit(net, train_x, train_y, title="Polynomial Regression"):
    plt.figure(figsize=(10, 8))
    plt.plot(train_x.data.numpy(), train_y.data.numpy(), 'o')
    plt.plot(train_x.data.numpy(), net(train_x.view(-1, 1)).data.numpy())
    plt.title(title)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()


def main():
    (a, b, c, d) = (0.2, 0.15, 0.1, 0.05)

    train_x, test_x, train_y, test_y = generate_noisy_data(a, b, c, d)
    net = Model()
    loss_fn = torch.nn.MSELoss();
    opt = torch.optim.SGD(net.parameters(), lr=0.0001)
    num_iterations = 10000

    neural_network(net, loss_fn, opt, train_x, train_y, num_iterations)
    plot_fit(net, train_x, train_y, title="Polynomial Regression Train")
    plot_fit(net, test_x, test_y, title="Polynomial Regression Test")
    print(net(test_x.view(-1, 1)))


if __name__ == "__main__":
    main()

输出：

loss: tensor(1880.3951)
loss: tensor(39.4567)
loss: tensor(33.8119)
loss: tensor(25.3780)
loss: tensor(21.3543)

png

png

tensor([[111.8431],
        [114.9060],
        [117.9690],
        [121.0319],
        [124.0948],
        [127.1578],
        [130.2207],
        [133.2837],
        [136.3466],
        [139.4095],
        [142.4725],
        [145.5354],
        [148.5984],
        [151.6613],
        [154.7242],
        [157.7872],
        [160.8501],
        [163.9130],
        [166.9760],
        [170.0389]], grad_fn=<AddmmBackward0>)